题目内容
5.函数f(x)=sinx+cosx的图象的一个对称中心到离它最近的对称轴的距离为$\frac{π}{2}$..分析 由两角和的余弦函数公式化简可得f(x)=$\sqrt{2}$sin(x+$\frac{π}{4}$),求得函数周期,从而得解.
解答 解:∵f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
∴T=$\frac{2π}{1}$=2π,
∴函数f(x)=sinx+cosx的图象的一个对称中心到离它最近的对称轴的距离为$\frac{T}{4}$=$\frac{2π}{4}$=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题主要考查三角函数的周期的计算,要求熟练掌握三角函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
13.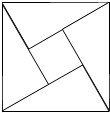 如图,大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛撒一枚幸运小花朵,则小花朵落在小正方形内的概率为( )
如图,大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛撒一枚幸运小花朵,则小花朵落在小正方形内的概率为( )
 如图,大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛撒一枚幸运小花朵,则小花朵落在小正方形内的概率为( )
如图,大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛撒一枚幸运小花朵,则小花朵落在小正方形内的概率为( )| A. | $\frac{1}{17}$ | B. | $\frac{2}{17}$ | C. | $\frac{3}{17}$ | D. | $\frac{4}{17}$ |
20.若复数x2-1+(x+1)i是纯虚数(i是虚数单位,x∈R),则x=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |