题目内容
已知函数f(x)=cos(2x-
)+2sin(x-
)cos(x-
),x∈R
(Ⅰ)将f(x)化为f(x)=Asin(ωx+φ)+b,(A>0,ω>0,|φ|<π);
(Ⅱ)若对任意x∈[-
,
],都有f(x)≥a成立,求a的取值范围;
(Ⅲ)若将y=f(x)的图象先纵坐标不变,横坐标变为原来的2倍,后向左平移
个单位得到函数y=g(x)的图象,求函数y=g(x)-
在区间[-2π,4π]内所有零点之和.
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
(Ⅰ)将f(x)化为f(x)=Asin(ωx+φ)+b,(A>0,ω>0,|φ|<π);
(Ⅱ)若对任意x∈[-
| π |
| 12 |
| π |
| 2 |
(Ⅲ)若将y=f(x)的图象先纵坐标不变,横坐标变为原来的2倍,后向左平移
| π |
| 6 |
| 1 |
| 3 |
(I)f(x)=cos(2x-
)+2sin(x-
)cos(x-
)
=cos(2x-
)+sin(2x-
)…(2分)
=
cos2x+
sin2x-cos2x…(4分)
=
sin2x-
cos2x
=sin(2x-
)…(6分)
(II)若对任意x∈[-
,
],都有f(x)≥a成立,则只需fmin(x)≥a即可
∵-
≤x≤
,∴-
≤2x-
≤
,…(8分)
∴当2x-
=-
即x=-
时,
f(x)有最小值即fmin(x)=f(-
)=-
故求a的取值范围为:a≤-
…(10分)
(III)依题意可得:g(x)=sinx
由g(x)-
=0得sinx=
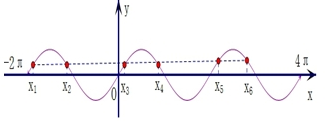
由图可知,原函数有6个零点:x1,x2,x3,x4,x5,x6根据对称性有:
=-
,
=
,
=
从而,所有零点和为:x1+x2+x3+x4+x5+x6=3π…(14分)
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
=cos(2x-
| π |
| 3 |
| π |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
(II)若对任意x∈[-
| π |
| 12 |
| π |
| 2 |
∵-
| π |
| 12 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴当2x-
| π |
| 6 |
| π |
| 3 |
| π |
| 12 |
f(x)有最小值即fmin(x)=f(-
| π |
| 12 |
| ||
| 2 |
故求a的取值范围为:a≤-
| ||
| 2 |
(III)依题意可得:g(x)=sinx
由g(x)-
| 1 |
| 3 |
| 1 |
| 3 |
由图可知,原函数有6个零点:x1,x2,x3,x4,x5,x6根据对称性有:
| x1+x2 |
| 2 |
| 3π |
| 2 |
| x3+x4 |
| 2 |
| π |
| 2 |
| x5+x6 |
| 2 |
| 5π |
| 2 |
从而,所有零点和为:x1+x2+x3+x4+x5+x6=3π…(14分)


练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 。
。 的周期;
的周期; 上的减区间;
上的减区间;
 ,
, ,求
,求 的值。
的值。





