题目内容
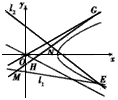
已知双曲线C的两条渐近线都过原点,且都以点A(| 2 |
(1)求双曲线C的方程;
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为
| 2 |
分析:(1)设双曲线的渐近线为y=kx,由d=
=1,解得k=±1,再由点A关于y=x对称点的坐标为(0,
),能求出双曲线C的方程.
(2)设直线ly=k(x-
)(0<k<1),依题意B点在平行的直线l′上,且l与l′间的距离为
,设直线l′y=kx+m,应有
=
,由此能求出k的值及此时B点的坐标.
|
| ||
|
| 2 |
(2)设直线ly=k(x-
| 2 |
| 2 |
|
| ||
|
| 2 |
解答:解:(1)设双曲线的渐近线为y=kx,由d=
=1,解得k=±1
即渐近线为y=±x,又点A关于y=x对称点的坐标为(0,
)
∴a=
=b,所求双曲线C的方程为y2-x2=2.
(2)设直线ly=k(x-
)(0<k<1),
依题意B点在平行的直线l′上,且l与l′间的距离为
设直线l′y=kx+m,应有
=
,
化简得m2+2
km=2②
把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由△=4m2k2-4(k2-1)(m2-2)=0
可得m2+2k2=2③
②、③两式相减得k=
m,代入③得m2=
,解得m=
,k=
,
此时x=
-2
,y=
,故B(2
,
).
|
| ||
|
即渐近线为y=±x,又点A关于y=x对称点的坐标为(0,
| 2 |
∴a=
| 2 |
(2)设直线ly=k(x-
| 2 |
依题意B点在平行的直线l′上,且l与l′间的距离为
| 2 |
设直线l′y=kx+m,应有
|
| ||
|
| 2 |
化简得m2+2
| 2 |
把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由△=4m2k2-4(k2-1)(m2-2)=0
可得m2+2k2=2③
②、③两式相减得k=
| 2 |
| 2 |
| 5 |
| ||
| 5 |
2
| ||
| 5 |
此时x=
| -mk |
| k2-1 |
| 2 |
| 10 |
| 2 |
| 10 |
点评:本题考查轨迹方程的求法和求k的值及此时B点的坐标.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用双曲线的性质,合理地进行等价转化.

练习册系列答案
相关题目
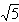 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,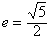 。
。