题目内容
一个圆柱和一个圆锥的母线相等，底面半径也相等，则侧面积之比是 ________．
2：1
分析：设圆锥、圆柱的母线为l，底面半径为r，求出圆锥、圆柱的侧面积，即可求出比值．
解答：设圆锥、圆柱的母线为l，底面半径为r，
所以圆锥的侧面积为：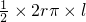
=πrl
圆柱的侧面积为：2πrl
所以圆柱和圆锥的侧面积的比为：2：1
故答案为：2：1
点评：本题考查圆锥，圆柱的侧面积的求法，考查计算能力，是基础题．
分析：设圆锥、圆柱的母线为l，底面半径为r，求出圆锥、圆柱的侧面积，即可求出比值．
解答：设圆锥、圆柱的母线为l，底面半径为r，
所以圆锥的侧面积为：
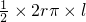=πrl圆柱的侧面积为：2πrl
所以圆柱和圆锥的侧面积的比为：2：1
故答案为：2：1
点评：本题考查圆锥，圆柱的侧面积的求法，考查计算能力，是基础题．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等，这时圆柱、圆锥、球的体积之比为（ ）
| A、1：2：3 | B、2：1：3 | C、3：1：2 | D、3：2：1 |
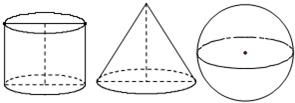如图，一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等，这时圆柱、圆锥、球的体积之比为
