Question

已知m∈R，复数z=+(m²+2m-3)i,当m为何值时，（1）z∈R；（2）z是纯虚数；（3）z对应的点位于复平面第二象限；（4）z对应的点在直线x+y+3=0上.

Answer 1

（1）m=-3（2）m=0或m=2（3）m＜-3或1＜m＜2（4）m=0或m=-1±

解析:

（1）当z为实数时,则有m²+2m-3=0且m-1≠0

得m=-3,故当m=-3时，z∈R.

（2）当z为纯虚数时,则有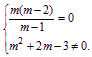

解得m=0，或m=2.

∴当m=0或m=2时，z为纯虚数.

（3）当z对应的点位于复平面第二象限时,

则有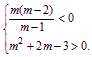

解得m＜-3或1＜m＜2，故当m＜-3或1＜m＜2时，z对应的点位于复平面的第二象限.

（4）当z对应的点在直线x+y+3=0上时,

则有+,

得=0，解得m=0或m=-1±.

∴当m=0或m=-1±时，z对应的点在直线x+y+3=0上.