��Ŀ����
����Ŀ�������ڳ���k��k��N* �� k��2����q��d��ʹ����������{an}����  �������{an}Ϊ���αȲ����С������г���k��q��d�ֱ�����γ����αȡ��β������{bn}Ϊ���αȲ����С���
�������{an}Ϊ���αȲ����С������г���k��q��d�ֱ�����γ����αȡ��β������{bn}Ϊ���αȲ����С���
��1����{bn}������γ����αȡ��β�ֱ�Ϊ1��3��q��3�� �ٵ�q=0ʱ����b2016��
�ڵ�q=1ʱ����{bn}��ǰ3n���ΪS3n �� ������ʽ ![]() ��n��N*���������ʵ���˵�ȡֵ��Χ��
��n��N*���������ʵ���˵�ȡֵ��Χ��
��2����{bn}Ϊ�ȱ����У�������Ϊb����д����������������{bn}����˵�����ɣ�
���𰸡�
��1���⣺�ٷ���һ����{bn}������γ����αȡ��β�ֱ�Ϊ1��3��0��3����b2014=0��b2013=0����b2015=b2014+3=3����b2016=b2015+3=6��
����������{bn}������γ����αȡ��β�ֱ�Ϊ1��3��0��3��
��b1=1��b2=4��b3=7��b4=0��b3=0��b5=b4+3=3��b6=b5+3=6��b7=0��b6=0����
�൱n��4ʱ��{bn}������Ϊ3���������У�
��b2016=b6=6��
�ڷ���һ����{bn}������γ����αȡ��β�ֱ�Ϊ1��3��1��3��
��b3n+2��b3n��1=��b3n+1+d����b3n��1=��qb3n+d����b3n��1=[q��b3n��1+d��+d]��b3n��1=2d=6��
��{b3n��1}����b2=4Ϊ���6Ϊ����ĵȲ����У�
�֡�b3n��2+b3n��1+b3n=��b3n��1��d��+b3n��1+��b3n��1+d��=3b3n��1����S3n=��b1+b2+b3��+��b4+b5+b6��+��+��b3n��2+b3n��1+b3n��= 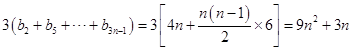 ����
���� ![]() ����
���� ![]() ����
���� ![]() ����ˡݣ�cn��max��
����ˡݣ�cn��max��
�� ![]() ��
��
��n=1ʱ��3n2��2n��2��0��c1��c2����n��2ʱ��3n2��2n��2��0��cn+1��cn��
��c1��c2��c3�������ࣨcn��max=c2=14��
��ˡ�14���æˡ�[14��+�ޣ���
����������{bn}������γ����αȡ��β�ֱ�Ϊ1��3��1��3��
��b3n+1=b3n����b3n+3��b3n=b3n+3��b3n+1=2d=6����{b3n}������Ϊb3=7������Ϊ6�ĵȲ����У�
�� ![]() ��
��
��֪{bn}��ɾ��{b3n}�����ԭ����˳��һ������Ϊ1����Ϊ3�ĵȲ����У��� ![]() ����
���� ![]() ��
��
����ͬ����һ��
��2���⣺����һ����{bn}�Ķγ����αȡ��β�ֱ�Ϊk��q��d��
��ȱ�����{bn}�Ĺ���Ϊ ![]() ���ɵȱ����е�ͨ�ʽ��
���ɵȱ����е�ͨ�ʽ�� ![]() ��
��
��m��N*ʱ��bkm+2��bkm+1=d����bqkm+1��bqkm=bqkm��q��1��=d���������q=1����d=0��bn=b��
����q��1���� ![]() ����qkmΪ��������q=��1��kΪż����d=��2b��
����qkmΪ��������q=��1��kΪż����d=��2b�� ![]() ��
��
�����飬����������{bn}��ͨ�ʽΪbn=b�� ![]() ��
��
����������{bn}�Ķγ����αȡ��β�ֱ�Ϊk��q��d��
����k=2����b1=b��b2=b+d��b3=��b+d��q��b4=��b+d��q+d��
�� ![]() ����b+d=bq����
����b+d=bq���� ![]() ���ã�b+d��q2=��b+d��q+d��
���ã�b+d��q2=��b+d��q+d��
������ʽ���� ![]() ��
�� ![]() ����bn=b��
����bn=b�� ![]() ��������������⣮
��������������⣮
����k��3����b1=b��b2=b+d��b3=b+2d��
�� ![]() ���ã�b+d��2=b��b+2d������d=0����bn=b���������ʺ����⣮
���ã�b+d��2=b��b+2d������d=0����bn=b���������ʺ����⣮
���Ϣ٢ڣ�����������{bn}��ͨ�ʽΪbn=b�� ![]()
����������1���ٷ���һ����{bn}������γ����αȡ��β�ɵ�b2014=0��b2013=0������b2015=b2014+3��b2016=b2015+3���ɣ� ������������{bn}������γ����αȡ��βb1=1��b2=4��b3=7��b4=0��b3=0��b5=b4+3=3��b6=b5+3=6��b7=0��b6=0����bn}������Ϊ3���������м��ɣ�
�ڷ���һ����{bn}������γ����αȡ��βb3n+2��b3n��1=��b3n+1+d����b3n��1=��qb3n+d����b3n��1=[q��b3n��1+d��+d]��b3n��1=2d=6��{b3n��1}�ǵȲ����У��֡�b3n��2+b3n��1+b3n=��b3n��1��d��+b3n��1+��b3n��1+d��=3b3n��1 �� ������S3n
����������{bn}������γ����αȡ��β�b3n+1=b3n �� ��b3n+3��b3n=b3n+3��b3n+1=2d=6����{b3n}������Ϊb3=7������Ϊ6�ĵȲ����м��ɣ���2������һ����{bn}�Ķγ����αȡ��β�ֱ�Ϊk��q��d���ȱ����е�ͨ�ʽ�� ![]() ��
��
��m��N*ʱ��bkm+2��bkm+1=d����bqkm+1��bqkm=bqkm��q��1��=d�����������q=1����d=0��bn=b������q��1���� ![]() ����qkmΪ��������q=��1��kΪż����d=��2b��
����qkmΪ��������q=��1��kΪż����d=��2b�� ![]() ������������{bn}�Ķγ����αȡ��β�ֱ�Ϊk��q��d������k=2����b1=b��b2=b+d��b3=��b+d��q��b4=��b+d��q+d����
������������{bn}�Ķγ����αȡ��β�ֱ�Ϊk��q��d������k=2����b1=b��b2=b+d��b3=��b+d��q��b4=��b+d��q+d���� ![]() ����b+d=bq����
����b+d=bq���� ![]() ���ã�b+d��q2=��b+d��q+d����õ�d ���ɢ���k��3����b1=b��b2=b+d��b3=b+2d����
���ã�b+d��q2=��b+d��q+d����õ�d ���ɢ���k��3����b1=b��b2=b+d��b3=b+2d���� ![]() ����õ�d ���ɣ�
����õ�d ���ɣ�
�����㾫����������Ҫ�����˵ȱ����еĻ������ʵ����֪ʶ�㣬��Ҫ����{an}Ϊ�ȱ����У����±�ɵȲ����еĶ�Ӧ��ɵȱ�����;{an}���ǵȲ��������ǵȱ�����== {an}�Ǹ��Ϊ��ij����в�����ȷ�����⣮

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
