题目内容
【题目】函数f(x)=xlnx-a(x-1)2-x,g(x)=lnx-2a(x-1),其中常数a∈R.
(Ⅰ)讨论g(x)的单调性;
(Ⅱ)当a>0时,若f(x)有两个零点x1,x2(x1<x2),求证:在区间(1,+∞)上存在f(x)的极值点x0,使得x0lnx0+lnx0-2x0>0.
【答案】(Ⅰ)见解析 (Ⅱ)x0=e2
【解析】试题分析:(Ⅰ) ![]() 讨论a与0的大小;(Ⅱ)由第一问得当a>0时,在区间(0,1]上,f(x)<0是显然的,即在此区间上f(x)没有零点;又由于f(x)有两个零点,则必然f(x)在区间(1,+∞)上有两个零点x1,x2(x1<x2),讨论
讨论a与0的大小;(Ⅱ)由第一问得当a>0时,在区间(0,1]上,f(x)<0是显然的,即在此区间上f(x)没有零点;又由于f(x)有两个零点,则必然f(x)在区间(1,+∞)上有两个零点x1,x2(x1<x2),讨论![]() 与1的大小,构造函数解出
与1的大小,构造函数解出![]() 的值;
的值;
试题解析:
(Ⅰ)解:函数g(x)的定义域为(0,+∞),导函数为![]() .
.
①当a≤0时,g′(x)>0恒成立,g(x)在定义域(0,+∞)上是增函数;
②当a>0时, ![]() ,并且,
,并且,
在区间(0, ![]() )上,g′(x)>0,∴g(x)在(0,
)上,g′(x)>0,∴g(x)在(0, ![]() )是增函数;
)是增函数;
在区间(![]() ,+∞)上,g′(x)<0,∴g(x)在区间(
,+∞)上,g′(x)<0,∴g(x)在区间(![]() ,+∞)上是减函数.
,+∞)上是减函数.
(Ⅱ)证明:当a>0时,在区间(0,1]上,f(x)<0是显然的,即在此区间上f(x)没有零点;又由于f(x)有两个零点,则必然f(x)在区间(1,+∞)上有两个零点x1,x2(x1<x2),
f′(x)=lnx-2a(x-1),由(Ⅰ)知,f′(x)在区间(0, ![]() )上是增函数,在区间(
)上是增函数,在区间(![]() ,+∞)上是减函数.
,+∞)上是减函数.
①若![]() ,则
,则![]() ,在区间(1,+∞)上,f′(x)是减函数,f′(x)≤f′(1)=0,f(x)在(1,+∞)上单调递减,不可能有两个零点,所以必然有
,在区间(1,+∞)上,f′(x)是减函数,f′(x)≤f′(1)=0,f(x)在(1,+∞)上单调递减,不可能有两个零点,所以必然有![]() .
.
②当![]() 时,在区间(1,
时,在区间(1, ![]() )上,f′(x)是增函数,f′(x)>f′(1)=0;
)上,f′(x)是增函数,f′(x)>f′(1)=0;
在区间(![]() ,+∞)上,f′(x)是减函数.依题意,必存在实数x0,使得在区间(
,+∞)上,f′(x)是减函数.依题意,必存在实数x0,使得在区间(![]() ,x0)上,f′(x)>0,f(x)是增函数;在区间(x0,+∞)上,f′(x)<0,f(x)是减函数.此时x0>1,且x0是f(x)的极大值点.
,x0)上,f′(x)>0,f(x)是增函数;在区间(x0,+∞)上,f′(x)<0,f(x)是减函数.此时x0>1,且x0是f(x)的极大值点.
所以f(x0)>0,且f′(x0)=0,即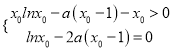 消去a得到x0lnx0+lnx0-2x0>0(x0>1).
消去a得到x0lnx0+lnx0-2x0>0(x0>1).
设F(x)=xlnx+lnx-2x(x>1),![]() .
.
∵![]() ,∴x>1时,F′(x)单调递增.又F′(1)=0,
,∴x>1时,F′(x)单调递增.又F′(1)=0,
∴x>1时,F′(x)>0.∴x>1时,F(x)单调递增.
又F(1)=-2<0,F(e2)=2>0.∴存在x0=e2>1满足题意.
亦可直接观察得到,x0=e2时,e2lne2+lne2-2e2=2>0,满足题意.
点睛: 本题主要考查了利用导数研究函数的单调性和极值、最值,考查了分类讨论的思想,属于难题.证明不等式往往是根据题意构造新函数,转化为求函数的最值,本题中因为导函数的零点不能直接求出,可通过设出零点,再证明函数在其两侧的单调性,说明其为最小值点,证其大于零.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案【题目】已知函数f(x)=x2﹣2|x﹣a|(a∈R).
(1)若函数f(x)为偶函数,求a的值;
(2)当a>0时,若对任意的x∈[0,+∞),不等式f(x﹣1)≤2f(x)恒成立,求实数a的取值范围.
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
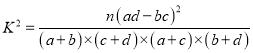 ,n=a+b+c+d.
,n=a+b+c+d.