题目内容
定义在R上的连续可导函数y=f(x),其导函数为y=f'(x),下列条件是“f(x)在R上单调递增”的充分不必要条件的是
- A.f'(x)≥0
- B.xf'(x)>0
- C.f(x+1)>f(x)
- D.(e-x)'+f'(x)>0
D
分析:欲判断各选项条件是不是“f(x)在R上单调递增”的充分不必要条件,从两个方面考察:(1)首先分清条件和结论.(2)再看条件能否推出结论,结论能否推出条件.
解答:对于A:若f'(x)=0满足“f'(x)≥0”,但f(x)在R上是常数函数,不是单调递增,故A错;
对于B:若x<0,则f'(x)<0,f(x)在(-∞,0)上单调递减,故B错;
对于C:若f(x)在R上单调递增,则f(x+1)>f(x),得出f(x+1)>f(x)是f(x)在R上单调递增的必要条件,故C错;
对于D:若(e-x)'+f'(x)>0,?[(e-x)+f(x)]′>0,
?f'(x)>0,?f(x)在R上单调递增,
反之不成立,
故(e-x)'+f'(x)>0是“f(x)在R上单调递增”的充分不必要条件.
在所出答案中只有D满足要求
故选D.
点评:判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
分析:欲判断各选项条件是不是“f(x)在R上单调递增”的充分不必要条件,从两个方面考察:(1)首先分清条件和结论.(2)再看条件能否推出结论,结论能否推出条件.
解答:对于A:若f'(x)=0满足“f'(x)≥0”,但f(x)在R上是常数函数,不是单调递增,故A错;
对于B:若x<0,则f'(x)<0,f(x)在(-∞,0)上单调递减,故B错;
对于C:若f(x)在R上单调递增,则f(x+1)>f(x),得出f(x+1)>f(x)是f(x)在R上单调递增的必要条件,故C错;
对于D:若(e-x)'+f'(x)>0,?[(e-x)+f(x)]′>0,
?f'(x)>0,?f(x)在R上单调递增,
反之不成立,
故(e-x)'+f'(x)>0是“f(x)在R上单调递增”的充分不必要条件.
在所出答案中只有D满足要求
故选D.
点评:判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
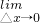
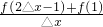 的值为
的值为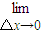
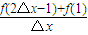 的值为( )
的值为( )