题目内容
用列举法表示下列集合:(1)A={x |x∈N,![]() ∈N};
∈N};
(2)B={x|![]() ∈N,x∈N};
∈N,x∈N};
(3)C={y|y=-x2+6,x∈N,y∈N};
(4)D={(x,y)|y=-x2+6,x∈N,y∈N};
答案:
解析:
提示:
解析:
| 解:(1)当x=0,6,8这三个自然数时,
∴A= {0,6,8} (2)由(1)知,B={1,3,9}. (3)由y=-x2+6,x∈N,y∈N知,y≤6, ∴x=0,1,2时,y=6,5,2符合题意. ∴C={2,5,6}. (4)点(x,y)满足条件y=-x2+6,x∈N,y∈N,则有
∴D={(0,6),(1,5),(2,2)} |
提示:
| 首先,应充分注意四个集合的各自特点:
集合A中的元素是自然数x,它必须满足条件 集合B中的元素是自然数 集合C中的元素是自然数y,它必须满足的条件是二次函数y=-x2+6(x∈N)的函数值的取值范围. 集合D中的元素是点,这些点必须满足的条件是它们在二次函数y=-x2+6的图象上,且横坐标、纵坐标都必须是自然数. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
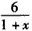 ∈Z},求M;
∈Z},求M;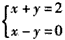 的解集;
的解集;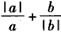 (a,b∈R)所确定的实数集合.
(a,b∈R)所确定的实数集合.