题目内容
设an是公差不为零的等差数列,Sn为其前n项和,满足a22+a32=a42+a52,S7=7(1)求数列an的通项公式及前n项和Sn;
(2)试求所有的正整数m,使得
| amam+1 | am+2 |
分析:(1)先把已知条件用a1及d表示,然后联立方程求出a1,d代入等差数列的通项公式及前n项和公式可求.
(2)先把已知化简可得
=2m-9+
,然后结合数列an的通项公式可寻求m满足的条件.
(2)先把已知化简可得
| am•am+1 |
| am+2 |
| 8 |
| 2m-3 |
解答:解:(1)由题意可得
联立可得a1=-5,d=2
∴an=-5+(n-1)×2=2n-7,sn=-5n+
×2=n2-6n
(2)由(1)知
=
=2m-9+
若使为数列an中的项
则
必需为整数,且m为正整数
m=2,m=1;
m=1时不满足题意,(a1=-5是最小值)故舍去.
所以m=2.
|
联立可得a1=-5,d=2
∴an=-5+(n-1)×2=2n-7,sn=-5n+
| n(n-1) |
| 2 |
(2)由(1)知
| amam+1 |
| am+2 |
| (2m-7)•(2m-5) |
| 2m-3 |
| 8 |
| 2m-3 |
则
| 8 |
| 2m-3 |
m=2,m=1;
m=1时不满足题意,(a1=-5是最小值)故舍去.
所以m=2.
点评:本题主要考查了等差数列的通项公式及前n项和的公式,解题的重点是要熟练掌握基本公式,并能运用公式,还要具备一定的运算能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
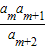 为数列an中的项.
为数列an中的项.