题目内容
已知,a>b>c,若 是3a与
是3a与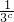 的等比中项,且
的等比中项,且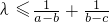 恒成立,则λ的最大值是________.
恒成立,则λ的最大值是________.
4
分析:根据 是3a与
是3a与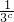 的等比中项,由等比中项概念列式得到a-c=1,把
的等比中项,由等比中项概念列式得到a-c=1,把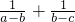 通分后运用基本不等式的性质求出其最小值,结合
通分后运用基本不等式的性质求出其最小值,结合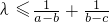 恒成立可求λ的最大值.
恒成立可求λ的最大值.
解答:由 是3a与
是3a与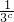 的等比中项,得:
的等比中项,得: ,
,
即3a-c=3,所以,a-c=1.
因为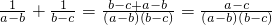 =
=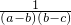 ,
,
由a>b>c,所以a-b>0,b-c>0.
则0<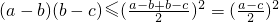 =
= ,
,
所以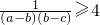
即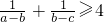
又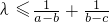 恒成立,
恒成立,
所以λ≤4.
所以λ的最大值是4.
故答案为4.
点评:本题考查了等比数列的性质,考查了利用基本不等式求最值,想到把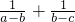 通分计算是该题的突破点,此题是中档题.
通分计算是该题的突破点,此题是中档题.
分析:根据
 是3a与
是3a与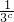 的等比中项,由等比中项概念列式得到a-c=1,把
的等比中项,由等比中项概念列式得到a-c=1,把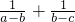 通分后运用基本不等式的性质求出其最小值,结合
通分后运用基本不等式的性质求出其最小值,结合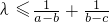 恒成立可求λ的最大值.
恒成立可求λ的最大值.解答:由
 是3a与
是3a与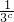 的等比中项,得:
的等比中项,得: ,
,即3a-c=3,所以,a-c=1.
因为
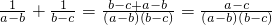 =
=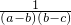 ,
,由a>b>c,所以a-b>0,b-c>0.
则0<
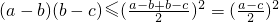 =
= ,
,所以
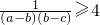
即
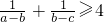
又
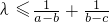 恒成立,
恒成立,所以λ≤4.
所以λ的最大值是4.
故答案为4.
点评:本题考查了等比数列的性质,考查了利用基本不等式求最值,想到把
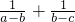 通分计算是该题的突破点,此题是中档题.
通分计算是该题的突破点,此题是中档题. 
练习册系列答案
相关题目
 ,b
,b ,c
,c ,若a//b,(a+b)
,若a//b,(a+b) (a-c),则
(a-c),则 的值为 .
的值为 .