题目内容
(2012•怀柔区二模)y=(sinx+cosx)2-1是( )
分析:将函数表达式展开,结合同角三角函数基本关系和二倍角正弦公式,对给出的函数进行化简整理,然后根据三角函数的图象与性质进行判断,即可得到正确选项.
解答:解:y=(sinx+cosx)2-1=sin2x+2sinxcosx+cos2x-1=sin2x,
∵y=sin2x的周期为T=
=π,且f(-x)=sin(-2x)=-sin2x=-f(x)
∴函数y=(sinx+cosx)2-1是最小正周期为π的奇函数.
故选:D
∵y=sin2x的周期为T=
| 2π |
| 2 |
∴函数y=(sinx+cosx)2-1是最小正周期为π的奇函数.
故选:D
点评:本题考查三角函数的性质,但要借助三角恒等变换,在大多数三角函数性质的试题中往往要以三角恒等变换为工具,把三角函数式化为一个角的一个三角函数,再根据基本的三角函数的性质对所给的三角函数的性质作出结论.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
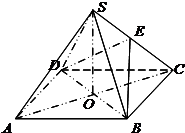 (2012•怀柔区二模)如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(2012•怀柔区二模)如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.