题目内容
（2012•怀柔区二模）如图，在四棱锥S-ABCD中，底面ABCD是正方形，四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC上一点．（1）当E为侧棱SC的中点时，求证：SA∥平面BDE；
（2）求证：平面BED⊥平面SAC．
分析：（1）连接OE，当E为侧棱SC的中点时，OE为△SAC的中位线，所以SA∥OE，由此能够证明SA∥平面BDE．
（2）因为 SB=SD，O是BD中点，所以BD⊥SO，因为四边形ABCD是正方形，所以BD⊥AC，因为AC∩SO=O，所以BD⊥平面SAC．由此能够证明平面BDE⊥平面SAC．
（2）因为 SB=SD，O是BD中点，所以BD⊥SO，因为四边形ABCD是正方形，所以BD⊥AC，因为AC∩SO=O，所以BD⊥平面SAC．由此能够证明平面BDE⊥平面SAC．
解答：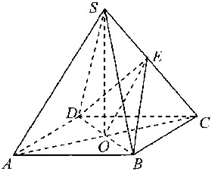
（本小题满分12分）
证明：（1）连接OE，当E为侧棱SC的中点时，OE为△SAC的中位线，
所以SA∥OE，（3分）
因为SA?平面BDE，OE?平面BDE，
所以SA∥平面BDE．（5分）
（2）因为SB=SD，O是BD中点，
所以BD⊥SO，（7分）
又因为四边形ABCD是正方形，所以BD⊥AC，（9分）
因为AC∩SO=O，所以BD⊥平面SAC．（11分）
又因为BD?平面BDE，
所以平面BDE⊥平面SAC．（12分）
（本小题满分12分）证明：（1）连接OE，当E为侧棱SC的中点时，OE为△SAC的中位线，
所以SA∥OE，（3分）
因为SA?平面BDE，OE?平面BDE，
所以SA∥平面BDE．（5分）
（2）因为SB=SD，O是BD中点，
所以BD⊥SO，（7分）
又因为四边形ABCD是正方形，所以BD⊥AC，（9分）
因为AC∩SO=O，所以BD⊥平面SAC．（11分）
又因为BD?平面BDE，
所以平面BDE⊥平面SAC．（12分）
点评：本题考查SA∥平面BDE和平面BED⊥平面SAC的证明，解题时要认真审题，仔细解答，注意把空间几何问题转化为平面几何问题进行求解．
练习册系列答案
相关题目