题目内容
已知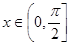 ,则函数
,则函数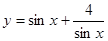 的最小值为( )
的最小值为( )
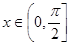 ,则函数
,则函数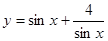 的最小值为( )
的最小值为( )| A.4 | B.5 | C.2 | D.3 |
B
试题分析:设
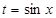 ,则
,则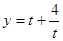 ,当
,当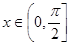 时,
时,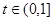 ,因为函数
,因为函数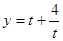 在
在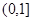 上单调递减,所以当
上单调递减,所以当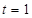 时,函数取得最小值,最小值为5.
时,函数取得最小值,最小值为5.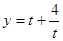 的单调性的判断和值域的求解方法,本题的易错点在基本不等式的使用条件和等号能否成立的判断.
的单调性的判断和值域的求解方法,本题的易错点在基本不等式的使用条件和等号能否成立的判断.
练习册系列答案
相关题目
题目内容
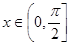 ,则函数
,则函数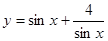 的最小值为( )
的最小值为( )| A.4 | B.5 | C.2 | D.3 |
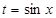 ,则
,则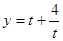 ,当
,当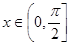 时,
时,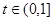 ,因为函数
,因为函数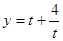 在
在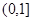 上单调递减,所以当
上单调递减,所以当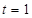 时,函数取得最小值,最小值为5.
时,函数取得最小值,最小值为5.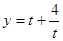 的单调性的判断和值域的求解方法,本题的易错点在基本不等式的使用条件和等号能否成立的判断.
的单调性的判断和值域的求解方法,本题的易错点在基本不等式的使用条件和等号能否成立的判断.