题目内容
已知 ,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).
,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).(1)求函数f(x)的解析式;
(2)求函数f(x)的值域.
【答案】分析:(1)由f(x)解析式得方程,把方程的解代入得关于a,b的方程组,求出a,b即可.
(2)由(1)得f(x)解析式,用分离系数法把式子进行整理,再用均值不等式求式子的范围,分成两类得到两个范围,取并集.
解答:解:(1)依已知条件可知方程f(x)-x+12=0即为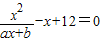 ,因为x1=3,x2=4是上述方程的解,
,因为x1=3,x2=4是上述方程的解,
所以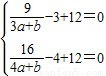 ,解得
,解得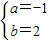 ,
,
所以函数的解析式为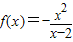
(2)因为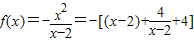 ,
,
当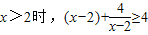 ,当且仅当x=4时取等号,所以y≤-8
,当且仅当x=4时取等号,所以y≤-8
当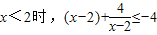 ,当且仅当x=0时取等号,所以y≥0
,当且仅当x=0时取等号,所以y≥0
所以函数f(x)的值域为(-∞,-8]∪[0,+∞).
点评:用待定系数法求函数解析式是一种常用的,重要的方法,是基本技能,傎域就是由自变量的范围得到整个式子的范围,利用均值不等式时,应注意一定二正三相等.
(2)由(1)得f(x)解析式,用分离系数法把式子进行整理,再用均值不等式求式子的范围,分成两类得到两个范围,取并集.
解答:解:(1)依已知条件可知方程f(x)-x+12=0即为
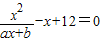 ,因为x1=3,x2=4是上述方程的解,
,因为x1=3,x2=4是上述方程的解,所以
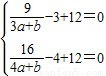 ,解得
,解得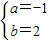 ,
,所以函数的解析式为
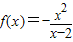
(2)因为
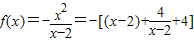 ,
,当
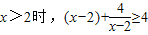 ,当且仅当x=4时取等号,所以y≤-8
,当且仅当x=4时取等号,所以y≤-8当
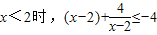 ,当且仅当x=0时取等号,所以y≥0
,当且仅当x=0时取等号,所以y≥0所以函数f(x)的值域为(-∞,-8]∪[0,+∞).
点评:用待定系数法求函数解析式是一种常用的,重要的方法,是基本技能,傎域就是由自变量的范围得到整个式子的范围,利用均值不等式时,应注意一定二正三相等.

练习册系列答案
相关题目
 ,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).
,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数). ,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).
,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数). ,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).
,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数). ,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).
,且方程f(x)-x+12=0有两个实根为x1=3,x2=4(这里a、b为常数).