题目内容
设A(x1,y1)为椭圆
答案:
解析:
解析:
| 证明:设椭圆参数方程为:
∵A(x1,y1)在椭圆上 ∴ ∴直线l的方程为:
∴d=
∴ ∴得证 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
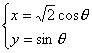 (θ为参数)
(θ为参数)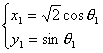
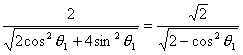
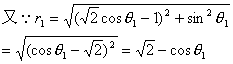
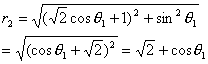
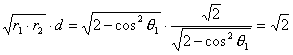 (常数)
(常数)