题目内容
已知抛物线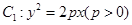 的焦点
的焦点 以及椭圆
以及椭圆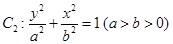 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆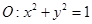 上.
上.
(1)求抛物线 和椭圆
和椭圆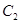 的标准方程;
的标准方程;
(2)过点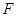 的直线交抛物线
的直线交抛物线 于
于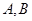 两不同点,交
两不同点,交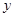 轴于点
轴于点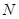 ,已知
,已知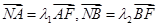 ,求
,求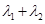 的值;
的值;
(3)直线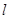 交椭圆
交椭圆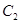 于
于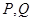 两不同点,
两不同点,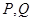 在
在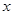 轴的射影分别为
轴的射影分别为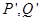 ,
,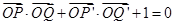 ,若点
,若点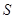 满足
满足 ,证明:点
,证明:点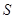 在椭圆
在椭圆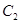 上.
上.
【答案】
(1)抛物线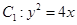 ,
,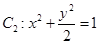 .(2)-1.(3)求出点S的坐标,然后代入椭圆方程即可证明
.(2)-1.(3)求出点S的坐标,然后代入椭圆方程即可证明
【解析】
试题分析:(1)由抛物线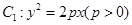 的焦点
的焦点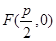 在圆
在圆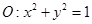 上得:
上得: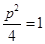 ,
,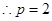 ,∴抛物线
,∴抛物线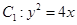 2分
2分
同理由椭圆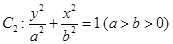 的上、下焦点
的上、下焦点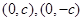 及左、右顶点
及左、右顶点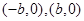 均在圆
均在圆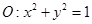 上可解得:
上可解得: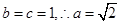 .得椭圆
.得椭圆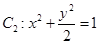 . 4分
. 4分
(2)设直线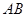 的方程为
的方程为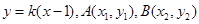 ,则
,则 .
.
联立方程组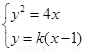 ,消去
,消去 得:
得:
 且
且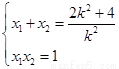 5分
5分
由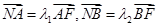 得:
得: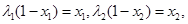
整理得: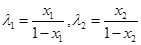
 .
8分
.
8分
(3)设 ,则
,则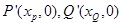
由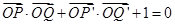 得
得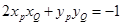 ;①
;① 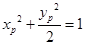 ;②
;②
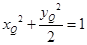 ;③ 11分
;③ 11分
由①+②+③得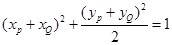
∴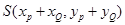 满足椭圆
满足椭圆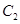 的方程,命题得证. 13分
的方程,命题得证. 13分
考点:本题考查了抛物线、椭圆的综合运用
点评:解答圆锥曲线问题时,应根据其几何特征熟练的转化为数量关系(如方程、函数),再结合代数方法解答,这就要学生在解决问题时要充分利用数形结合、设而不求、弦长公式及韦达定理综合思考,重视对称思想、函数与方程思想、等价转化思想的应用。

练习册系列答案
相关题目
 的焦点
的焦点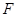 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆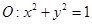 上.
上.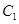 和椭圆
和椭圆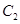 的标准方程;
的标准方程;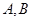 两不同点,交
两不同点,交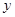 轴于点
轴于点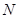 ,已知
,已知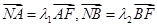 ,求
,求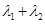 的值;
的值;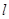 交椭圆
交椭圆 两不同点,
两不同点,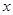 轴的射影分别为
轴的射影分别为 ,
, ,若点
,若点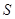 满足
满足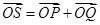 ,证明:点
,证明:点 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程; 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则
 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程; 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则 是否为定值?若是,求出其值;若不是,说明理由.
是否为定值?若是,求出其值;若不是,说明理由.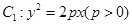 的焦点
的焦点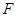 以及椭圆
以及椭圆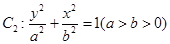 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆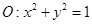 上.
上. 和椭圆
和椭圆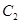 的标准方程;
的标准方程;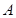 、
、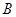 两不同点,交
两不同点,交 轴于点
轴于点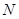 ,已知
,已知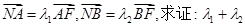 为定值.
为定值. 交椭圆
交椭圆 两不同点,
两不同点, 轴的射影分别为
轴的射影分别为 ,
, ,若点
,若点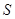 满足:
满足: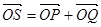 ,证明:点
,证明:点