Question

【题目】已知方程x2＋y2－2(m＋3)x＋2(1－4m2)y＋16m4＋9＝0表示一个圆．

(1) 求实数m的取值范围；

(2) 求该圆半径r的取值范围；

(3) 求该圆心的纵坐标的最小值．

Answer 1

【答案】（1）；（2）；（3）-1.

【解析】试题分析：（1）利用方程表示圆的条件D2+E2-4F>0，建立不等式，即可求出实数m的取值范围；
（2）利用圆的半径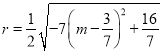，，利用配方法结合（1）中实数m的取值范围，即可求出该圆半径r的取值范围；
（3）根据x2+y2-2（m+3）x+2（1-4m2）y+16m4+9=0，确定圆的圆心坐标，再消去参数，得y＝4(x－3)2－1，根据（1）中实数m的取值范围，即可求得最小值.．

试题解析：

(1) 方程表示圆的等价条件是D2＋E2－4F>0，即有4(m＋3)2＋4(1－4m2)2－4(16m4＋9)>0，

解得－<m<1.

(2) 半径，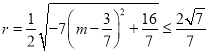

解得.

(3) 设圆心坐标为(x，y)，则消去m，得y＝4(x－3)2－1.

由于，所以.

故圆心的纵坐标y＝4(x－3)2－1， ，所以最小值是－1.