题目内容
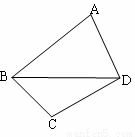
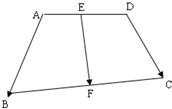如图，在任意四边形ABCD中，E，F分别是AD，BC的中点，若. |
| AB |
. |
| CD |
. |
| EF |
. |
| 0 |
分析：由E、F分别是AD、BC的中点，我们根据相反向量的定义，易得
+
=
，
+
=
，利用平面向量加法的三角形法则，我们易将向量
分别表示为
+
+
和
+
+
的形式，两式相加后，易得到结论．
| EA |
| ED |
| 0 |
| FB |
| FC |
| 0 |
| EF |
| AB |
| BF |
| EA |
| ED |
| DC |
| CF |
解答：解：如图，
∵E、F分别是AD、BC的中点，
∴
+
=
，
+
=
，
又∵
+
+
+
=
，
∴
=
+
+
①
同理
=
+
+
②
由①+②得，
2
=
+
+
+
+
+
=
+
．
∴λ=2．
故答案为：2
∵E、F分别是AD、BC的中点，
∴
| EA |
| ED |
| 0 |
| FB |
| FC |
| 0 |
又∵
| BF |
| BF |
| FE |
| EA |
| 0 |
∴
| EF |
| AB |
| BF |
| EA |
同理
| EF |
| ED |
| DC |
| CF |
由①+②得，
2
| EF |
| AB |
| DC |
| EA |
| ED |
| BF |
| CF |
| AB |
| DC |
∴λ=2．
故答案为：2
点评：本题考查的知识点是向量加减混合运算及其几何意义，向量的三角形法则，其中根据向量加法的三角形法则对待证结论中的向量进行分解是解答本题的关键，属基础题．
练习册系列答案
相关题目
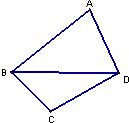已知一颗粒子等可能地落入如图所示的四边形ABCD内的任意位置，如果通过大量的实验发现粒子落入△BCD内的频率稳定在
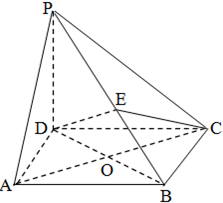如图，在四棱锥P-ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC=2，
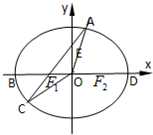（A题）如图，在椭圆
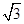，E是PB上任意一点．
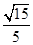，若E为PB的中点，求EC与平面PAB所成角的正弦值．
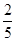附近，那么点A和点C到直线BD的距离之比约为 