题目内容
直线 与圆
与圆 没有公共点,则过点
没有公共点,则过点 的直线与椭圆
的直线与椭圆 的交点的个数是( )
的交点的个数是( )
| A.至多一个 | B.2个 | C.1个 | D.0个 |
B
解析试题分析:直线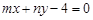 与圆
与圆 没有公共点,
没有公共点,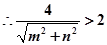 ,
,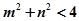
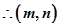 在圆
在圆 内部,在椭圆
内部,在椭圆 内部,所以过
内部,所以过 的直线与椭圆有两个交点
的直线与椭圆有两个交点
考点:直线与圆,椭圆的位置关系
点评:判断直线与椭圆的交点个数,需判断直线过的定点与椭圆的位置关系,求解本题利用到了数形结合法,此法在一些选择填空题目中经常用到,可使计算简化,难度适中

练习册系列答案
相关题目
若直线 过圆
过圆 的圆心,则
的圆心,则 的值为( )
的值为( )
A. | B. | C. | D. |
圆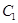 :
:  与圆
与圆 :
:  的位置关系是
的位置关系是
| A.外离 | B.相交 | C.内切 | D.外切 |
圆 关于
关于 对称的圆的方程是( )
对称的圆的方程是( )
A. | B. |
C. | D. |
若圆 :
: 关于直线
关于直线 对称,则
对称,则 的最小值是( )
的最小值是( )
| A.2 | B. | C. | D. |
已知直角坐标系中圆 方程为
方程为 ,
, 为圆内一点(非圆心),
为圆内一点(非圆心),
那么方程 所表示的曲线是———————— ( )
所表示的曲线是———————— ( )
A.圆 |
B.比圆 半径小,与圆 半径小,与圆 同心的圆 同心的圆 |
C.比圆 半径大与圆 半径大与圆 同心的圆 同心的圆 |
| D.不一定存在 |
过原点且倾斜角为 的直线被圆学
的直线被圆学 所截得的弦长为
所截得的弦长为
A. | B.2 | C. | D.2 |
若直线y=x-2被圆 所截得的弦长为
所截得的弦长为 ,则实数
,则实数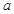 的值为( )
的值为( )
A.-1或 | B.1或3 | C.-2或6 | D.0或4 |
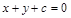 上,则点(m,c)不满足下列哪个方程( )
上,则点(m,c)不满足下列哪个方程( )


