题目内容
广东省汕头市日前提出,要提升市民素质和城市文明程度,促进经济发展有大的提速,努力实现“幸福汕头”的共建共享.现随机抽取50位市民,对他们的幸福指数进行统计分析,得到如下分布表:| 幸福级别 | 非常幸福 | 幸福 | 不知道 | 不幸福 |
| 幸福指数(分) | 90 | 60 | 30 | |
| 人数(个) | 19 | 21 | 7 | 3 |
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.
【答案】分析:(I)由数学期望(即平均值)的定义,结合图表可得答案;
(II)可得ξ的可能取值为0、1、2、3,分别求其概率,即可得其分布列;
(III)方法一,求对立事件n≥m+60的概率,进而由P=1-P1可得答案,方法二,直接列举出符合n<m+60的情况,由古典概型的公式可得答案.
解答:解:(Ⅰ)记Ex表示这50位市民幸福指数的数学期望,
∴ .…(1分)
.…(1分)
(Ⅱ)ξ的可能取值为0、1、2、3 …(2分)
 …(3分)
…(3分)
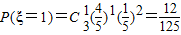 …(4分)
…(4分)
 …(5分)
…(5分)
 …(6分)
…(6分)
∴ξ分布列为
…(7分)
(Ⅲ)方法一:设所有满足条件的对立事件n≥m+60的概率为P1
①满足m=0且n=60的事件数为: …(8分)
…(8分)
②满足m=0且n=90的事件数为: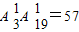 …(9分)
…(9分)
③满足m=30且n=90的事件数为: …(10分)
…(10分)
∴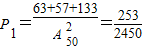 …(11分)
…(11分)
所以满足条件n<m+60的事件的概率为 .…(12分)
.…(12分)
方法二:基本事件的总数为
满足条件n<m+60的有如下各种情况:
①满足m=0时,n=0,30的事件数为: …(8分)
…(8分)
②满足m=30时,n=0,30,60的事件数为: …(9分)
…(9分)
③满足m=60时,n=0,30,60,90的事件数为: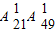 …(10分)
…(10分)
④满足m=90时,n=0,30,60,90的事件数为: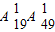 …(11分)
…(11分)
所以 …(12分)
…(12分)
点评:本题考查离散型随机变量及其分布列,涉及数学期望的求解,属中档题.
(II)可得ξ的可能取值为0、1、2、3,分别求其概率,即可得其分布列;
(III)方法一,求对立事件n≥m+60的概率,进而由P=1-P1可得答案,方法二,直接列举出符合n<m+60的情况,由古典概型的公式可得答案.
解答:解:(Ⅰ)记Ex表示这50位市民幸福指数的数学期望,
∴
 .…(1分)
.…(1分)(Ⅱ)ξ的可能取值为0、1、2、3 …(2分)
 …(3分)
…(3分)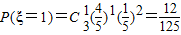 …(4分)
…(4分) …(5分)
…(5分) …(6分)
…(6分)∴ξ分布列为
| ξ | 1 | 2 | 3 | |
| P | 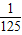 |  | 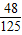 |  |
(Ⅲ)方法一:设所有满足条件的对立事件n≥m+60的概率为P1
①满足m=0且n=60的事件数为:
 …(8分)
…(8分)②满足m=0且n=90的事件数为:
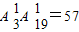 …(9分)
…(9分)③满足m=30且n=90的事件数为:
 …(10分)
…(10分)∴
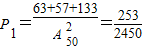 …(11分)
…(11分)所以满足条件n<m+60的事件的概率为
 .…(12分)
.…(12分)方法二:基本事件的总数为

满足条件n<m+60的有如下各种情况:
①满足m=0时,n=0,30的事件数为:
 …(8分)
…(8分)②满足m=30时,n=0,30,60的事件数为:
 …(9分)
…(9分)③满足m=60时,n=0,30,60,90的事件数为:
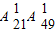 …(10分)
…(10分)④满足m=90时,n=0,30,60,90的事件数为:
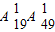 …(11分)
…(11分)所以
 …(12分)
…(12分)点评:本题考查离散型随机变量及其分布列,涉及数学期望的求解,属中档题.

练习册系列答案
相关题目
广东省汕头市日前提出,要提升市民素质和城市文明程度,促进经济发展有大的提速,努力实现“幸福汕头”的共建共享.现随机抽取50位市民,对他们的幸福指数进行统计分析,得到如下分布表:
(I)求这50位市民幸福指数的数学期望(即平均值);
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.
| 幸福级别 | 非常幸福 | 幸福 | 不知道 | 不幸福 |
| 幸福指数(分) | 90 | 60 | 30 | |
| 人数(个) | 19 | 21 | 7 | 3 |
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.
广东省汕头市日前提出,要提升市民素质和城市文明程度,促进经济发展有大的提速,努力实现“幸福汕头”的共建共享.现随机抽取50位市民,对他们的幸福指数进行统计分析,得到如下分布表:
(I)求这50位市民幸福指数的数学期望(即平均值);
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.
| 幸福级别 | 非常幸福 | 幸福 | 不知道 | 不幸福 |
| 幸福指数(分) | 90 | 60 | 30 | |
| 人数(个) | 19 | 21 | 7 | 3 |
(11)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数.求ξ的分布列;
(III)从这50位市民中,先随机选一个人.记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P.