题目内容
曲线C上任一点到定点(0,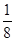 )的距离等于它到定直线
)的距离等于它到定直线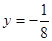 的距离.
的距离.
(1)求曲线C的方程;
(2)经过P(1,2)作两条不与坐标轴垂直的直线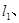
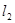 分别交曲线C于A、B两点,且
分别交曲线C于A、B两点,且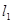 ⊥
⊥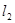 ,设M是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
,设M是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
(1)y=2x2;
(2)M轨迹是抛物线,故存在一定点和一定直线,使得M到定点的距离等于它到定直线的距离。所求的定点为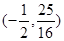 ,定直线方程为y=
,定直线方程为y=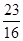 .
.
解析试题分析:
思路分析:(1)曲线C上任一点到定点(0,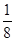 )的距离等于它到定直线
)的距离等于它到定直线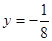 的距离.所以,由抛物线的定义,其方程为
的距离.所以,由抛物线的定义,其方程为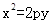 ,而
,而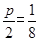 ,所以,y=2x2;
,所以,y=2x2;
(2)利用“参数法” 得到y=4x2+4x+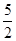 ,根据图象的平移变换得到结论:定点为
,根据图象的平移变换得到结论:定点为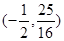 ,定直线方程为y=
,定直线方程为y=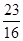 .
.
解:(1)因为,利用抛物线的定义,确定得到y=2x2;
(2)设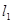 :y-2=k(x-1)(k≠0)
:y-2=k(x-1)(k≠0) 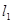 :y=2=
:y=2=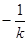
由 得2x2-kx+k-2=0
得2x2-kx+k-2=0
同理得B点坐标为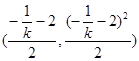
∴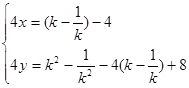
消去k得:y=4x2+4x+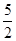 ………9分
………9分
M轨迹是抛物线,故存在一定点和一定直线,使得M到定点的距离等于它到定直线的距离。将抛物线方程化为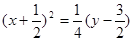 ,此抛物线可看成是由抛物线
,此抛物线可看成是由抛物线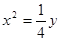 左移
左移 个单位,上移
个单位,上移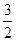 个单位得到的,而抛物线
个单位得到的,而抛物线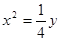 的焦点为(0,
的焦点为(0,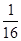 ),准线为y=-
),准线为y=-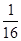 .∴所求的定点为
.∴所求的定点为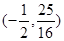 ,定直线方程为y=
,定直线方程为y=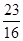 .
.
考点:抛物线方程,直线与抛物线的位置关系。
点评:难题,利用“直接法”可确定得到抛物线方程。利用“参数法”求得抛物线方程,通过研究焦点、准线等,达到确定“存在性”的目的。

练习册系列答案
相关题目
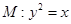 与曲线
与曲线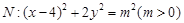 相交于
相交于 、
、 、
、 、
、 四个点.
四个点.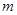 的取值范围;
的取值范围;  的面积的最大值及此时对角线
的面积的最大值及此时对角线 与
与 的交点坐标.
的交点坐标.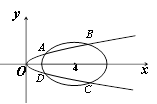
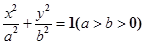 的两个顶点,
的两个顶点, 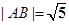 ,直线AB的斜率为
,直线AB的斜率为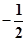 .求椭圆的方程;(2)设直线
.求椭圆的方程;(2)设直线 平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,
平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,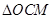 的面积等于
的面积等于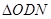 的面积.
的面积.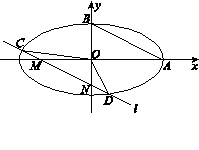
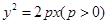 的焦点为F,经过点F的直线与抛物线交于A、B两点.
的焦点为F,经过点F的直线与抛物线交于A、B两点.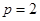 ,求线段
,求线段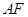 中点M的轨迹方程;
中点M的轨迹方程; ,当焦点为
,当焦点为 时,求
时,求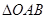 的面积;
的面积;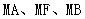 的斜率成等差数列.
的斜率成等差数列. 的中心在原点,焦点在
的中心在原点,焦点在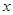 轴上,离心率
轴上,离心率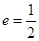 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线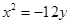 的焦点.
的焦点.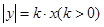 的交点为
的交点为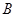 、
、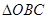 面积的最大值.
面积的最大值.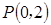 的直线
的直线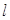 与抛物线
与抛物线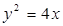 交于
交于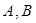 两点,
两点,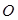 为坐标原点.
为坐标原点.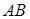 为直径的圆经过原点
为直径的圆经过原点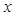 轴于点
轴于点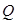 ,求
,求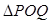 面积的取值范围.
面积的取值范围.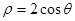 ,曲线C2的参数方程为
,曲线C2的参数方程为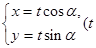 为参数)。
为参数)。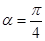 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标; 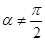 ,当
,当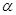 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.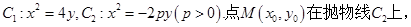
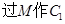
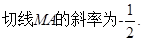
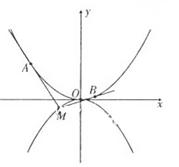
 ;
;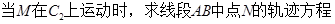
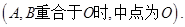
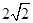 ,离心率
,离心率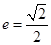 .
.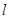 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与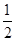 ,求直线
,求直线