题目内容
曲线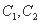 都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线
都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线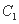 的短轴,并且是曲线
的短轴,并且是曲线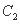 的长轴 . 直线
的长轴 . 直线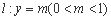 与曲线
与曲线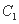 交于A,D两点(A在D的左侧),与曲线
交于A,D两点(A在D的左侧),与曲线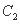 交于B,C两点(B在C的左侧).
交于B,C两点(B在C的左侧).
(1)当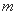 =
=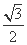 ,
,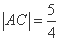 时,求椭圆
时,求椭圆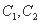 的方程;
的方程;
(2)若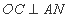 ,求
,求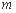 的值.
的值.
【答案】
(1)C1 ,C2的方程分别为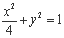 ,
,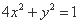 ;(2)
;(2)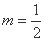 .
.
【解析】
试题分析:(1)解:设曲线C1的方程为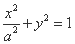 ,C2的方程为
,C2的方程为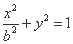 (
(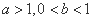 )…2分
)…2分
∵C1 ,C2的离心率相同,∴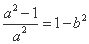 ,∴
,∴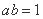 ,
3分
,
3分
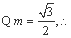 令
令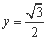 代入曲线方程,则
代入曲线方程,则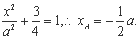
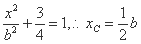 .
.
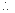 当
当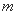 =
=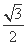 时,A
时,A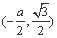 ,C
,C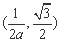 .……………5分
.……………5分
又∵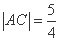 ,
,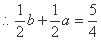 .由
.由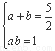 ,且
,且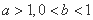 ,解得
,解得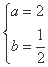 6分
6分
∴C1 ,C2的方程分别为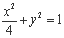 ,
,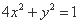 .
7分
.
7分
(2)令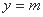 代入曲线方程,
代入曲线方程,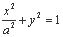 ,得
,得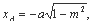
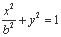 ,得
,得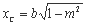 9分
9分
由于 ,所以
,所以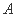 (-
(-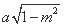 ,m),
,m),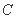 (
(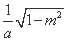 ,m) .
10分
,m) .
10分
由于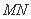 是曲线
是曲线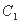 的短轴,所以
的短轴,所以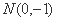 .
.
∵OC⊥AN,
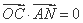 (
( ).
11分
).
11分
∵ =(
=(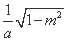 ,m),
,m),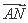 =(
=(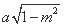 ,-1-m),
,-1-m),
代入(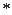 )并整理得2m2+m-1=0,
12分
)并整理得2m2+m-1=0,
12分
∴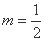 或
或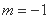 (舍负) ,∴
(舍负) ,∴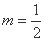 . 14分
. 14分
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系,平面向量的坐标运算。
点评:难题,求椭圆的标准方程,主要运用了椭圆的几何性质,注意明确焦点轴和a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)利用向量垂直,数量积为0,确定得到m的方程。

练习册系列答案
相关题目
 上的最大值为
上的最大值为 ,求实数b的值;
,求实数b的值;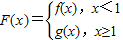 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.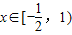 上的最大值为
上的最大值为 ,求实数b的值;
,求实数b的值;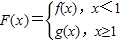 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.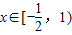 上的最大值为
上的最大值为 ,求实数b的值;
,求实数b的值;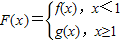 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.