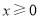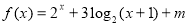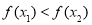题目内容
已知:如图,等腰直角三角形 的直角边
的直角边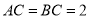 ,沿其中位线
,沿其中位线 将平面
将平面 折起,使平面
折起,使平面 ⊥平面
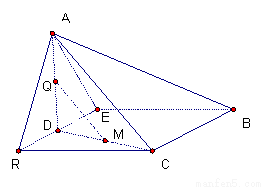
⊥平面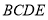 ,得到四棱锥
,得到四棱锥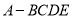 ,设
,设 、
、 、
、 、
、 的中点分别为
的中点分别为 、
、 、
、 、
、 .
.



(1)求证: 、
、 、
、 、
、 四点共面;
四点共面;
(2)求证:平面 平面
平面 ;
;
(3)求异面直线 与
与 所成的角.
所成的角.
(1)见解析;(2)见解析;(3)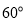 .
.
【解析】
试题分析:(1)要证四点共面,只需找到一个平面,这四个点都在这个平面内,用确定平面的方法,两条平行线确定一个平面,即可证出;(2)要证明两个平面垂直,只需证明其中一个平面经过另一个平面的一条垂线即可,也就是只需证线面垂直即可,而要证线面垂直,只需证明这条直线垂直平面内的两条相交直线,这样,一步步寻找成立的条件即可;(3)求异面直线所成角,先平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成角就是异面直线所成角或其补角,再放入三角形中计算即可.
试题解析:(1)由条件有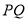 为
为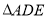 的中位线,
的中位线,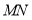 为梯形
为梯形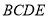 的中位线
的中位线

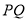 ∥
∥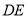 ,
,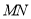 ∥
∥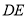

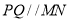

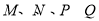 四点共面 3分
四点共面 3分
(2)证明:由等腰直角三角形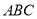 有
有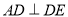 ,
,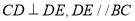
又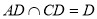 ,
,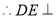 面
面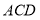 又
又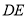 ∥
∥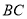

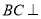 平面
平面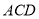 ,
,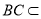 平面
平面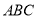
 平面
平面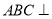 平面
平面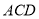 6分
6分
(3)由条件知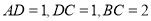
延长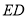 到
到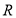 ,使
,使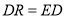 ,连结
,连结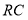 8分
8分
则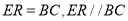 ,故
,故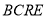 为平行四边形 10分
为平行四边形 10分

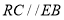 ,又
,又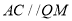

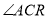 为异面直线BE与QM所成的角
为异面直线BE与QM所成的角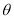 (或
(或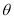 的补角) 11分
的补角) 11分
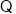
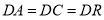 ,且三线两两互相垂直
,且三线两两互相垂直
∴由勾股定理得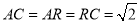 12分
12分
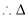 ACR为正三角形,
ACR为正三角形,
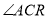 =
=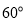 ,
, 异面直线
异面直线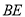 与
与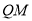 所成的角大小为
所成的角大小为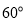 13分.
13分.
考点:1.平面的基本性质;2.平面与平面垂直的判定;3.异面直线及其所成的角.

练习册系列答案
相关题目