题目内容
先解答(Ⅰ),再通过结构类比解答(Ⅱ):
(Ⅰ)求证:tan(x+
)=
;
(Ⅱ) 设x∈R且f(x+π)=
,试问:f(x)是周期函数吗?证明你的结论.
(Ⅰ)求证:tan(x+
| π |
| 4 |
| 1+tanx |
| 1-tanx |
(Ⅱ) 设x∈R且f(x+π)=
| 1+f(x) |
| 1-f(x) |
分析:(I)根据两角和的正切公式,把所给的等式的右边展开,利用特殊角的三角函数最后得到和右边的式子相等,等式得证.
(II)根据正切函数的周期性的证明方法,类比推理到抽象函数的周期性的证明方法,两次应用所给的等式.
(II)根据正切函数的周期性的证明方法,类比推理到抽象函数的周期性的证明方法,两次应用所给的等式.
解答:(Ⅰ)证明:tan(x+
)=
=
.
(Ⅱ)解:f(x)是以4π为其一个周期的周期函数.
f(x+2π)=f(x+π+π)=
=
=-
,
∴f(x+4π)=f[(x+2π)+2π]=-
=-
=f(x),
所以f(x)是周期函数,其中一个周期为4π.
| π |
| 4 |
tanx+tan
| ||
1-tanxtan
|
| 1+tanx |
| 1-tanx |
(Ⅱ)解:f(x)是以4π为其一个周期的周期函数.
f(x+2π)=f(x+π+π)=
| 1+f(x+π) |
| 1-f(x+π) |
1+
| ||
1-
|
| 1 |
| f(x) |
∴f(x+4π)=f[(x+2π)+2π]=-
| 1 |
| f(x+2π) |
| 1 | ||
-
|
所以f(x)是周期函数,其中一个周期为4π.
点评:本题考查两角和的正切公式和类比推理,本题解题的关键是掌握类比推理的一般步骤首先找出两类事物之间的相似性或一致性,再根据一类事物的性质去推测另一类事物的性质,得出一个明确的命题,本题是一个中档题目.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 ,并写出函数
,并写出函数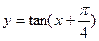 的最小正周期;
的最小正周期;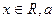 为非零常数,且
为非零常数,且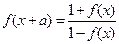 ,试问
,试问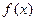 是周期函数吗?证明你的结论。
是周期函数吗?证明你的结论。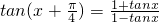 ;②用反证法证明:函数f(x)=tanx的最小正周期是π;
;②用反证法证明:函数f(x)=tanx的最小正周期是π;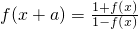 ,试问:f(x)是周期函数吗?证明你的结论.
,试问:f(x)是周期函数吗?证明你的结论.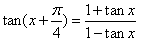 ;
;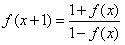 ,试问:f(x)是周期函数吗?证明你的结论。
,试问:f(x)是周期函数吗?证明你的结论。