题目内容
先解答(1),再通过类比解答(2):(1)①求证:tan(x+
| π |
| 4 |
| 1+tanx |
| 1-tanx |
(2)设x∈R,a为正常数,且f(x+a)=
| 1+f(x) |
| 1-f(x) |
分析:本题考查的知识点是类比推理,在由正切函数的周期性类比推理抽象函数的周期性时,我们常用的思路是:由正切函数的周期性,类比推理抽象函数的周期性;由正切函数的周期性的证明方法,类比推理抽象函数的周期性的证明方法.
解答:解:(1)①证明:tan(x+
)=
=
.
②假设T是函数f(x)=tanx的一个周期,且0<T<π,
则对任意x≠
+kπ,k∈Z,有tan(x+T)=tanx,令x=0得tanT=0,
而当0<T<π时,tanT≠0恒成立或无意义,矛盾,所以假设不成立,原命题成立.
(2)由(1)可类比出函数f(x)是周期函数,它的最小正周期是4a.
证明:因为f(x+2a)=f(x+a+a)=
=
=-
,
所以f(x+4a)=f[(x+2a)+2a]=-
=-
=f(x).
| π |
| 4 |
tanx+tan
| ||
1-tanxtan
|
| 1+tanx |
| 1-tanx |
②假设T是函数f(x)=tanx的一个周期,且0<T<π,
则对任意x≠
| π |
| 2 |
而当0<T<π时,tanT≠0恒成立或无意义,矛盾,所以假设不成立,原命题成立.
(2)由(1)可类比出函数f(x)是周期函数,它的最小正周期是4a.
证明:因为f(x+2a)=f(x+a+a)=
| 1+f(x+a) |
| 1-f(x+a) |
1+
| ||
1-
|
| 1 |
| f(x) |
所以f(x+4a)=f[(x+2a)+2a]=-
| 1 |
| f(x+2a) |
| 1 | ||
-
|
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).但类比推理的结论不一定正确,还需要经过证明,我们在进行类比推理时,一定要注意对结论进行进一步的论证,如果要证明一个结论是正确的,要经过严密的论证,但要证明一个结论是错误的,只需要举出一个反例.

练习册系列答案
相关题目
 ,并写出函数
,并写出函数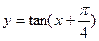 的最小正周期;
的最小正周期;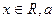 为非零常数,且
为非零常数,且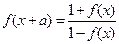 ,试问
,试问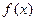 是周期函数吗?证明你的结论。
是周期函数吗?证明你的结论。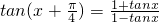 ;②用反证法证明:函数f(x)=tanx的最小正周期是π;
;②用反证法证明:函数f(x)=tanx的最小正周期是π;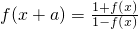 ,试问:f(x)是周期函数吗?证明你的结论.
,试问:f(x)是周期函数吗?证明你的结论.