题目内容
已知: 是
是 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, .
.
(Ⅰ)求角A的大小;
(Ⅱ)若 求
求 的长.
的长.
(Ⅰ) 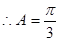 . (Ⅱ)
. (Ⅱ)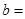
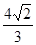 。
。
解析试题分析:(I)根据 .可得
.可得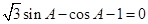 ,进一步转化可得
,进一步转化可得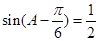 ,
,
从而可求出A值.
(II)再(I)的基础上可知在三角形ABC中,已知角A,B,边a,从而可利用正弦定理求b.
(Ⅰ)  =
=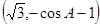 ……1分
……1分 =
=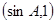 ……2分
……2分
∵
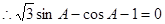 ……4分
……4分 ……6分
……6分
∵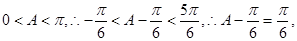 ……7分
……7分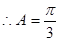 .……8分
.……8分
(Ⅱ)在 中,
中,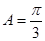 ,
,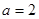 ,
,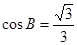
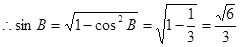 ……9分由正弦定理知:
……9分由正弦定理知: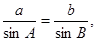 ……10分
……10分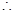
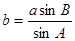 =
=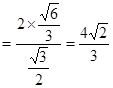 .
.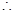
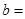
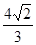 ……12分
……12分
考点:向量的数量积的坐标表示,两角差的正弦公式,给值求角,正弦定理.
点评:掌握向量的数量积的坐标表示是解决此问题的突破口,再利用两角差的正弦公式可求得A角,然后还要知道正弦定理可解决两类三角形问题:一是已知两边及一边的对角,二是知道两角及一边.

练习册系列答案
相关题目
已知向量m= ,n=
,n= .
.
(1)若m·n=1,求cos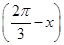 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
在△ 中,若
中,若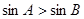 ,则
,则 与
与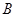 的大小关系为( )
的大小关系为( )
A.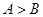 | B.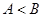 | C.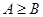 | D. 、 、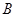 的大小关系不能确定 的大小关系不能确定 |
 ,
,
 的最小正周期,并求
的最小正周期,并求 上的最小值;
上的最小值; 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若 ,
, ,
, ,求
,求 .
. ,
,
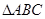 中,若
中,若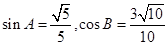 ,且
,且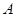 为锐角,求角
为锐角,求角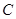 .
.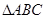 中,角
中,角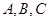 所对的边为
所对的边为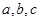 已知
已知 .
. 的值;
的值;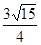 ,且
,且 ,求
,求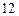 分)已知函数
分)已知函数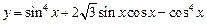 ,
,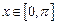 ,求该函数的单调递增区间。
,求该函数的单调递增区间。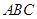 中,角
中,角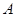 、
、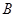 、
、 的对边分别为
的对边分别为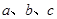 ,若
,若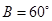 ,且
,且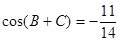 .
.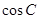 的值; (2)若
的值; (2)若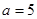 ,求△
,求△