题目内容
已知函数f(x)=kx-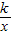 -2lnx,其中k∈R;
-2lnx,其中k∈R;(1)若函数f(x)在其定义域内为单调递增函数,求实数k的取值范围.
(2)若函数g(x)=
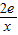 ,且k>0,若在[1,e]上至少存在一个x的值使f(x)>g(x)成立,求实数k的取值范围.
,且k>0,若在[1,e]上至少存在一个x的值使f(x)>g(x)成立,求实数k的取值范围.
【答案】分析:(1)因为f(x)在其定义域内的单调递增函数,所以f'(x)在(0,+∞)内满足f'(x)≥0恒成立,转化为求kx2-2x+k≥0对x∈(0,+∞)恒成立,然后利用分离参数法,转化为求函数的最值,即可求得实数k的取值范围.
(2)在[1,e]上至少存在一个x的值使f(x)>g(x)成立,等价于不等式f(x)-g(x)>0在[1,e]上有解,只需f(x)-g(x)的最大值大于0即可.
解答:解:(1)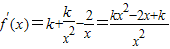 ,
,
因为f(x)在其定义域内的单调递增函数,
所以f'(x)在(0,+∞)内满足f'(x)≥0恒成立,
即kx2-2x+k≥0对x∈(0,+∞)恒成立,
亦即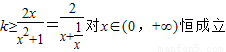 ,∴
,∴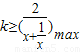 即可
即可
又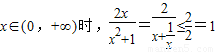 ,
,
当且仅当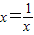 ,即x=1时取等号,∴使函数f(x)在其定义域内为单调增函数的实数k的取值范围是[1,+∞).
,即x=1时取等号,∴使函数f(x)在其定义域内为单调增函数的实数k的取值范围是[1,+∞).
(2)在[1,e]上至少存在一个x的值使f(x)>g(x)成立,等价于不等式f(x)-g(x)>0在[1,e]上有解,
设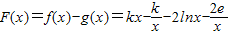 ,
,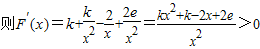 ,
,
∴F(x)为[1,e]上的增函数,F(x)max=F(e),
依题意需 ∴实数k的取值范围是
∴实数k的取值范围是 .
.
点评:本题主要考查用导数法研究函数的单调性,函数最值的应用.基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题,体现了转化的数学思想,很好的考查了学生的计算能力.
(2)在[1,e]上至少存在一个x的值使f(x)>g(x)成立,等价于不等式f(x)-g(x)>0在[1,e]上有解,只需f(x)-g(x)的最大值大于0即可.
解答:解:(1)
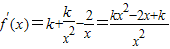 ,
,因为f(x)在其定义域内的单调递增函数,
所以f'(x)在(0,+∞)内满足f'(x)≥0恒成立,
即kx2-2x+k≥0对x∈(0,+∞)恒成立,
亦即
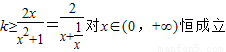 ,∴
,∴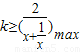 即可
即可又
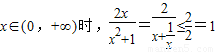 ,
,当且仅当
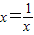 ,即x=1时取等号,∴使函数f(x)在其定义域内为单调增函数的实数k的取值范围是[1,+∞).
,即x=1时取等号,∴使函数f(x)在其定义域内为单调增函数的实数k的取值范围是[1,+∞).(2)在[1,e]上至少存在一个x的值使f(x)>g(x)成立,等价于不等式f(x)-g(x)>0在[1,e]上有解,
设
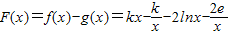 ,
,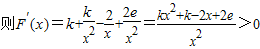 ,
,∴F(x)为[1,e]上的增函数,F(x)max=F(e),
依题意需
 ∴实数k的取值范围是
∴实数k的取值范围是 .
.点评:本题主要考查用导数法研究函数的单调性,函数最值的应用.基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题,体现了转化的数学思想,很好的考查了学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目