题目内容
设函数

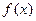 =cos(x+
=cos(x+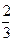 π)+cos
π)+cos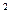
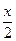 ,0<x<π
,0<x<π(1)求
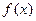 的值域;
的值域;(2)设三角形ABC的内角A、B、C的对边分别为a、b、c,若f(B)=1,b=1,c=
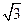 ,求边a的值
,求边a的值见解析
解:(1)f(x)=cosxcos
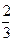 π-sinxsin
π-sinxsin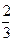 π+cosx+1
π+cosx+1=
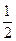 cosx-
cosx-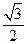 sinx+1=cos(x+
sinx+1=cos(x+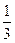 π)+1
π)+1由于0<x<π,所以
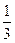 π<x+
π<x+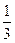 π<
π<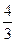 π, -1≤cos(x+
π, -1≤cos(x+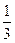 π)<
π)<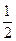
所以
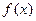 的值域为[0,
的值域为[0,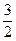 ).
).(2)因为f(B)=1,所以cos(B+
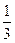 π)+1=1,又0<B<π,所以B=
π)+1=1,又0<B<π,所以B=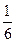 π.
π.由余弦定理得b²=a²+c²-2accosB,得a²-3a+2=0,
所以a=1或a=2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
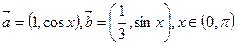
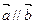 ,求
,求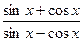 的值;
的值;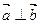 ,求
,求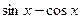 的值。
的值。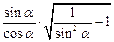 =" " ( )
=" " ( )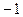
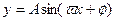 在同一周期内,当
在同一周期内,当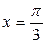 时有最大值2,当x=0时有最小值-2,那么函数的解析式为( )
时有最大值2,当x=0时有最小值-2,那么函数的解析式为( )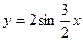
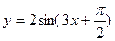
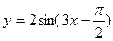
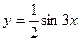
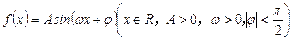 的图象如图所示,
的图象如图所示,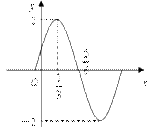
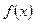 的解析式是__________________________
的解析式是__________________________  =
= 、Sin
、Sin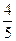 ,则角
,则角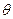 的终边落在直线( )上。
的终边落在直线( )上。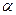 的顶点在原点,始边与
的顶点在原点,始边与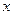 轴非负半轴重合,终边为射线
轴非负半轴重合,终边为射线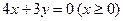 ,则
,则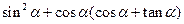 的值是
的值是
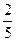
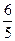
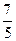
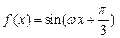 (
(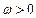 )的最小正周期为
)的最小正周期为 ,则该函数的图象
,则该函数的图象 ,0)对称
,0)对称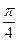 ,0)对称
,0)对称