题目内容
3.把函数y=2sinx图象上各点的横坐标缩短为原来的$\frac{1}{2}$,然后把所得的图象再向右平移$\frac{π}{6}$个单位,则所得图象对应的函数解析式为( )| A. | y=2sin($\frac{1}{2}x+\frac{π}{6}$) | B. | y=2sin(2x-$\frac{π}{3}$) | C. | y=sin($\frac{1}{2}x-\frac{π}{3}$) | D. | y=2sin(2x+$\frac{π}{3}$) |
分析 把图象上所有点的横坐标缩小到原来的$\frac{1}{2}$,得到y=2sin2x,再函数y=2sinx的图象上所有点向右移$\frac{π}{6}$个单位,得到y=2sin[2(x-$\frac{π}{6}$)],写出要求的结果.
解答 解:把图象上所有点的横坐标缩小到原来的$\frac{1}{2}$,得到y=2sin2x,
再函数y=2sin2x的图象上所有点向右平移$\frac{π}{6}$个单位,得到y=2sin[2(x-$\frac{π}{6}$)]=2sin(2x-$\frac{π}{3}$)对图象,
∴所求函数的解析式为:y=2sin(2x-$\frac{π}{3}$).
故选:B.
点评 本题考查三角函数图形的变换,注意在图象平移时,要看清楚函数的解析式中x的系数是不是1,若只考查图象变换,则一般先平移后伸缩,属于基本知识的考查.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
16.若存在实数x=x0,使得不等式ax>a-1不成立,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,+∞) |
11.记函数f(x)的导函数为f′(x),若f(x)对应的曲线在点(x0,f(x0))处的切线方程为y=-x+1,则( )
| A. | f′(x0)=2 | B. | f′(x0)=1 | C. | f′(x0)=0 | D. | f′(x0)=-1 |
18.已知集合A={x|-2<x<1},B={x|x2-2x≤0},则A∩B=( )
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-1<x≤1} | D. | {x|-2<x≤1} |
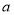 ,
,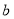 ,
, 是正数,求证:
是正数,求证: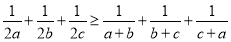 .
.  ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.