题目内容
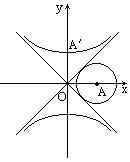
已知双曲线S的两条渐近线过坐标原点,且与以点A(2,0)为圆心,1为半径的圆相切,双曲线S的一个顶点A′与点A关于直线y=x对称,设直线l过点A,斜率为k.如图.
(1)求双曲线S的方程;
(2)当k=1时,在双曲线S的上支上,求点B,使其与直线l的距离为
.
解:(1)设双曲线方程为
=1(a＞0,b＞0).
∵A(,0)关于直线y=x对称的点为A′(0,
),
∴a=2,渐近线方程为y=±
x.
由y=
x与圆A:(x-
)2+y2=1相切得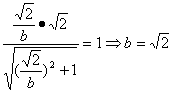
.
故双曲线方程为y2-x2=2.
(2)若B(x,
)是双曲线S的上支上到直线l:y=x-2的距离为
的点,
即
∴|
-x|=2,
+
-x=2.
移项平方解得x=
,
=2,
∴点B的坐标是(
,2).
练习册系列答案
相关题目
，0)为圆心，1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
；
，求斜率k的值及相应的点B的坐标．如图．
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与点A关于直线y=x对称.设直线l过点A，斜率为k.
；
，求斜率k的值及相应的点B的坐标，如图.
，0)为圆心、1为半径的圆相切，双曲线S的一个顶点
与点A关于直线y＝x对称．设直线l过点A，斜率为k．
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与A关于直线y=x对称，设直线l过点A，且斜率为k. 
；
，求斜率k的值及相应的点B的坐标.