题目内容
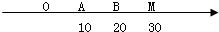如图，O为数轴的原点，A，B，M为数轴上三点，C为线段OM上的动点，设x表示C与原点的距离，y 表示C到A距离4倍与C道B距离的6倍的和．（1）将y表示成x的函数；
（2）要使y的值不超过70，x应该在什么范围内取值？
分析：（1）由题设描述CO=x，CA=|10-x|，CB=|20-x|，由y 表示C到A距离4倍与C道B距离的6倍的和，直接建立函数关系即可，由于解析式含有绝对值号，故可以将解析式转换成分段函数．
（2）对（1）中的函数进行研究利用其单调性与值域探讨x的取值范围即可．
（2）对（1）中的函数进行研究利用其单调性与值域探讨x的取值范围即可．
解答：解：（1）由题设，CO=x，CA=|10-x|，CB=|20-x|，
故y=4×|10-x|+6×|20-x|，x∈[0，30]
即y=
（2）令y≤70，
当x∈[0，10]时，由160-10x≤70得x≥9，故x∈[9，10]
当x∈（10，20]时，由80-2x≤70得x≥5，故x∈（10，20]
当x∈（20，30]时，由10x-160≤70得x≤23，故x∈（20，23]
综上知，x∈[9，23]
故y=4×|10-x|+6×|20-x|，x∈[0，30]
即y=
|
（2）令y≤70，
当x∈[0，10]时，由160-10x≤70得x≥9，故x∈[9，10]
当x∈（10，20]时，由80-2x≤70得x≥5，故x∈（10，20]
当x∈（20，30]时，由10x-160≤70得x≤23，故x∈（20，23]
综上知，x∈[9，23]
点评：本题考点是函数解析式的求解及常用方法，本题考查根据题设条件所给的关系建立函数解析式，然后再根据解析式解不等式，由于本题的解析式是一个分段型的，所以在解不等式时要分段求解，解出每一段上的不等式的解集，最后再将它们并起来．
练习册系列答案
相关题目
