题目内容
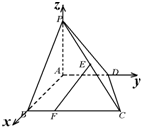 已知ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=1,BC=2,E为PC的中点,PA⊥平面ABCD,建立如图所示的空间直角坐标系.
已知ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=1,BC=2,E为PC的中点,PA⊥平面ABCD,建立如图所示的空间直角坐标系.(1)写出点E的坐标;
(2)能否在BC上找到一点F,使EF⊥CD?若能,请求出点F的位置,若不能,请说明理由;
(3)求证:平面PCB⊥平面PCD.
分析:(1)由题意可得:D(0,1,0)P(0,0,1),C(1,2,0),根据题意即可求出点E的坐标.
(2)假设能在BC上找到一点F,使EF⊥CD,设F(1,t,0),分别写出直线EF与CD所在的向量,利用向量的数量积为0,即可求出t的值.
(3)利用向量的数量积为0可得EF⊥PC,再证明线面垂直,进而证明面面垂直.
(2)假设能在BC上找到一点F,使EF⊥CD,设F(1,t,0),分别写出直线EF与CD所在的向量,利用向量的数量积为0,即可求出t的值.
(3)利用向量的数量积为0可得EF⊥PC,再证明线面垂直,进而证明面面垂直.
解答: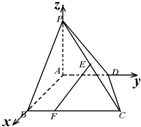 解:(1)由题意可得:D(0,1,0)P(0,0,1),C(1,2,0),
解:(1)由题意可得:D(0,1,0)P(0,0,1),C(1,2,0),
∵E为PC的中点,
∴E(
,1,
)(2分)
(2)设能在BC上找到一点F,使EF⊥CD,设F(1,t,0),
则
=(
,t-1,-
),并且
=(-1,-1,0),
∵EF⊥CD,
∴
•
=-
+1-t=0,
∴t=
,即存在点F(1,
,0)满足要求.(5分)
(3)∵
=(1,2,-1)
∴
•
=(
,-
,-
)•(1,2,-1)=0,
∴EF⊥PC(6分).
由(2)知:EF⊥CD,因为PC∩CD=C,
所以EF⊥平面PCD,
又∵EF?平面PCB,(7分)
∴平面PCB⊥平面PCD.(8分)
 解:(1)由题意可得:D(0,1,0)P(0,0,1),C(1,2,0),
解:(1)由题意可得:D(0,1,0)P(0,0,1),C(1,2,0),∵E为PC的中点,
∴E(
| 1 |
| 2 |
| 1 |
| 2 |
(2)设能在BC上找到一点F,使EF⊥CD,设F(1,t,0),
则
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| CD |
∵EF⊥CD,
∴
| EF |
| CD |
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵
| PC |
∴
| EF |
| PC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF⊥PC(6分).
由(2)知:EF⊥CD,因为PC∩CD=C,
所以EF⊥平面PCD,
又∵EF?平面PCB,(7分)
∴平面PCB⊥平面PCD.(8分)
点评:利用空间坐标系,求出相应直线的方向向量与平面的法向量,进而将空间线线的垂直问题,及线面的垂直问题,转化为向量夹角问题是解答本题的关键.

练习册系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,