题目内容
已知 ,
, ,且
,且
(1)求函数
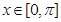 的单调增区间;
的单调增区间;
(2)证明无论 为何值,直线
为何值,直线 与函数
与函数 的图象不相切.
的图象不相切.
(1)单调增区间为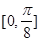 和
和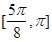 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)首先由向量的数量积及坐标运算得函数 的解析式,利用正弦函数的单调区间即可求得该函数的单调区间;(2)注意直线
的解析式,利用正弦函数的单调区间即可求得该函数的单调区间;(2)注意直线 的斜率为4,那么要证明无论
的斜率为4,那么要证明无论 为何值,直线
为何值,直线 与函数
与函数 的图象不相切,就只需通过求导说明函数的导数值不可能等于4即可.
的图象不相切,就只需通过求导说明函数的导数值不可能等于4即可.
试题解析:(1)∵ ,
, ,且
,且
∴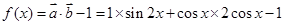 1分
1分
=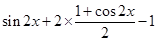 =
=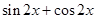
=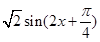 3分
3分
令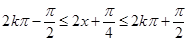 ,解之得
,解之得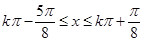 4分
4分
又∵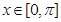 ∴
∴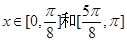
故函数
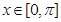 的单调增区间为
的单调增区间为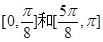 6分
6分
(2)∵  9分
9分
∴曲线 的切线斜率的取值范围为
的切线斜率的取值范围为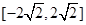
而直线 的斜率为
的斜率为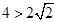 , 11分
, 11分
∴证明无论 为何值,直线
为何值,直线 与函数
与函数 的图象不相切 12分
的图象不相切 12分
考点:1、向量的数量积及坐标运算;2、三角变换及三角函数的单调区间;3、导数的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的最大值为
的最大值为 ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为 .
. 的解析式;
的解析式; ,求
,求 的值.
的值. .
.
 的图象(部分)如图所示.
的图象(部分)如图所示.
 的解析式;
的解析式; ,求函数
,求函数
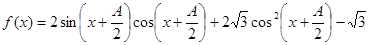 的单调递增区间.
的单调递增区间. =(2cos
=(2cos ,1),
,1), =(cos
=(cos sin2
sin2 =
= R.
R. [
[ ,
, ],求
],求 =
= (
( )与
)与 ,2),求函数
,2),求函数
 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数

 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像. <C<
<C< ,且
,且 =
= .
. +
+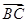 |=2,求
|=2,求 ,
,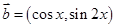 ,
,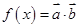 .(1)求
.(1)求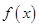 的最小正周期、最大值及
的最小正周期、最大值及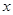 的集合;
的集合;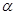 满足
满足 ,求
,求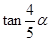 的值.
的值.