题目内容

设函数f(x)=｜1｜(x＞0).

（1）求f(x)的单调区间；

（2）是否存在正实数a,b(a＜b)，使函数f(x)的定义域为［a,b］时值域为［,］？若存在，求a,b的值;若不存在，请说明理由.

解:(1)∵f(x)=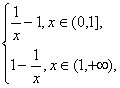

∴f(x)的递减区间为(0,1］，递增区间为(1,+∞).

（2）假使存在符合题设的a,b,则

当0＜a＜b≤1时，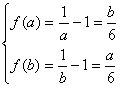

a=b(与a＜b矛盾）.

当0＜a＜1＜b时，f(1)=0∈［,］,∴a≤0＜b(这与a＞0矛盾）.

当1＜a＜b时，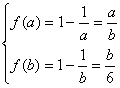

a,b是方程x2-6x+6=0的两根.

∴a=3-,b=3+3.

综上,存在a=3-,b=3+满足题意.

练习册系列答案
相关题目
已知向量
m
=(2cos
x
2
，1)，
n
=(sin
x
2
，1)（x∈R），设函数f(x)=
m
•
n
-1．
（1）求函数f（x）的值域；
（2）已知锐角△ABC的三个内角分别为A，B，C，若f(A)=
5
13
，f(B)=
3
5
，求f（C）的值．
设函数f(x)=
kx+2
x-1
的图象关于直线y=x对称．
（Ⅰ）求实数k的值；
（Ⅱ）若
lim
x→+∞
f(x)=a且f（|t|+2）＜f（4a），求实数t的取值范围．
设函数f(x)=
log
1
3
(x2-1) ， x＞0
e-x ，  x＜0
，则f(
1
f(2)
)=
e
e
．
设函数f(x)=
a2
x2+cosx-1(x∈(0，+∞))的导数为f′（x）．
（I）当a=1时，证明：f′（x）＞0；
（II）当a=1时，数列{an}满足：0＜a1＜1，且an+1=f（an），求证：0＜an+1＜an＜1；
（III）若y=f（x）的单调增函数，求正数a的取值范围．
（2008•如东县三模）设函数f(x)=lg(
2
x+1
-1)的定义域为集合A，函数g(x)=
1-|x+a|
的定义域为集合B．
（1）判定函数f（x）的奇偶性，并说明理由．
（2）问：a≥2是A∩B=∅的什么条件（充分非必要条件、必要非充分条件、充要条件、既非充分也非必要条件）？并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网