题目内容
设0<a<1,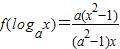 ,
,(Ⅰ)求f(x)的表达式,并指出其奇偶性、单调性(不必写出证明过程);
(Ⅱ)解关于x的不等式:f(ax)+f(-2)>f(2)+f(-ax)
(Ⅲ)(理)当n∈N时,比较f(n)与n的大小.
(文)若f(x)-4的值仅在x<2时取负数,求a的取值范围.
【答案】分析:(Ⅰ)令t=logax,则x=at,∴ ,从而可得函数f(x)的表达式;
,从而可得函数f(x)的表达式;
(Ⅱ)问题等价于f(ax)>f(2),从而ax>2,由于0<a<1,∴x<loga2;
(Ⅲ)将问题转化为f(n)= +…+(a2n-1+a)],再利用基本不等式可知
+…+(a2n-1+a)],再利用基本不等式可知 ,从而有f(n)≥n;若f(x)-4的值仅在x<2时取负数等价于f(x)<4时x<2恒成立,从而可解.
,从而有f(n)≥n;若f(x)-4的值仅在x<2时取负数等价于f(x)<4时x<2恒成立,从而可解.
解答:解:(Ⅰ)令t=logax,则x=at,∴ ,∴f(x)=
,∴f(x)= ),x∈R.(2分)
),x∈R.(2分)
∵f(-x)=f(x),∴奇函数.∵0<a<1,∴函数为增函数(2分)
(Ⅱ)∵f(ax)-f(2)>f(2)-f(ax)
∴f(ax)>f(2),ax>2,
∵0<a<1,∴x<loga2(4分)
(Ⅲ)(理料)f(1)=1,(1分)
当n≥2时,f(n)= …a2n-1,)
…a2n-1,)
= +…+(a2n-1+a)]>
+…+(a2n-1+a)]> (5分)
(5分)
或用数学归纳法证明:f(k+1)=af(k)+a-k>ak+ak-k∵0<a<1,
∴可令 ,∴
,∴
(文科)∵ (6分)
(6分)
点评:本题主要考查函数解析式的求解及函数性质的判断,同时考查利用基本不等式进行大小比较,有一定的综合性.
 ,从而可得函数f(x)的表达式;
,从而可得函数f(x)的表达式;(Ⅱ)问题等价于f(ax)>f(2),从而ax>2,由于0<a<1,∴x<loga2;
(Ⅲ)将问题转化为f(n)=
 +…+(a2n-1+a)],再利用基本不等式可知
+…+(a2n-1+a)],再利用基本不等式可知 ,从而有f(n)≥n;若f(x)-4的值仅在x<2时取负数等价于f(x)<4时x<2恒成立,从而可解.
,从而有f(n)≥n;若f(x)-4的值仅在x<2时取负数等价于f(x)<4时x<2恒成立,从而可解.解答:解:(Ⅰ)令t=logax,则x=at,∴
 ,∴f(x)=
,∴f(x)= ),x∈R.(2分)
),x∈R.(2分) ∵f(-x)=f(x),∴奇函数.∵0<a<1,∴函数为增函数(2分)
(Ⅱ)∵f(ax)-f(2)>f(2)-f(ax)
∴f(ax)>f(2),ax>2,
∵0<a<1,∴x<loga2(4分)
(Ⅲ)(理料)f(1)=1,(1分)
当n≥2时,f(n)=
 …a2n-1,)
…a2n-1,)=
 +…+(a2n-1+a)]>
+…+(a2n-1+a)]> (5分)
(5分)或用数学归纳法证明:f(k+1)=af(k)+a-k>ak+ak-k∵0<a<1,
∴可令
 ,∴
,∴
(文科)∵
 (6分)
(6分)点评:本题主要考查函数解析式的求解及函数性质的判断,同时考查利用基本不等式进行大小比较,有一定的综合性.

练习册系列答案
相关题目
设0<a<1,对于函数f(x)=
(0<x<π),下列结论正确的是( )
| sinx+a |
| sinx |
| A、有最大值而无最小值 |
| B、有最小值而无最大值 |
| C、有最大值且有最小值 |
| D、既无最大值又无最小值 |
设0<a<1,若x1=a,x2=ax1,x3=ax2,x4=ax3,…xn=axn-1,…则数列{xn}( )
| A、递增 | B、偶数项增,奇数项减 | C、递减 | D、奇数项增,偶数项减 |