题目内容
13.在四边形ABCD中,M为BD上靠近D的三等分点,且满足$\overrightarrow{AM}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则实数x,y的值分别为( )| A. | $\frac{1}{3}$,$\frac{2}{3}$ | B. | $\frac{2}{3}$,$\frac{1}{3}$ | C. | $\frac{1}{2}$,$\frac{1}{2}$ | D. | $\frac{1}{4}$,$\frac{3}{4}$ |
分析 可画出图形,根据向量加法、减法,及数乘的几何意义便有$\overrightarrow{AM}=\overrightarrow{AD}+\frac{1}{3}(\overrightarrow{AB}-\overrightarrow{AD})=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,这样根据平面向量基本定理便可得出x,y的值,从而找出正确选项.
解答 解:如图,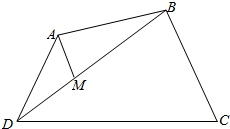
$\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\frac{1}{3}\overrightarrow{DB}$=$\overrightarrow{AD}+\frac{1}{3}(\overrightarrow{AB}-\overrightarrow{AD})=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$;
又$\overrightarrow{AM}=x\overrightarrow{AB}+y\overrightarrow{AD}$;
∴$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$.
故选:A.
点评 考查向量加法、减法,以及数乘的几何意义,以及向量的数乘运算,平面向量基本定理.

练习册系列答案
相关题目
4.若函数y=(a2-3a+3)ax是指数函数,则函数y=bx+2-a必过定点( )
| A. | (0,1) | B. | (-2,-1) | C. | (0,-2) | D. | (-2,-2) |
5.已知集合A={y|y=x2},B={x|y=lg(2-x),则A∩B=( )
| A. | A、[0,2] | B. | [0,2) | C. | (-∞,2] | D. | (-∞,2) |
3.函数f(x)=log2(-2x+4)的定义域是( )
| A. | {x|x>-2} | B. | {x|x≥-2} | C. | {x|x<2} | D. | {x|x≤-2} |