题目内容
已知函数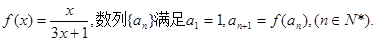
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和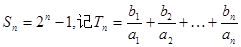 求Tn.
求Tn.
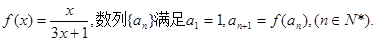
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和
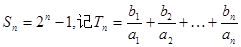 求Tn.
求Tn. (1)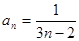 ; (2)Tn=(3n-5)·2n+5
; (2)Tn=(3n-5)·2n+5
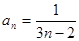 ; (2)Tn=(3n-5)·2n+5
; (2)Tn=(3n-5)·2n+5(1)由题意得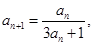 即
即 ,又
,又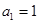 ,所以
,所以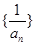 是首项a1,公差d=3的等差数列,根据等差数列的通项公式得
是首项a1,公差d=3的等差数列,根据等差数列的通项公式得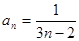 ;(2)由
;(2)由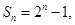 可求出
可求出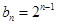 ,所以
,所以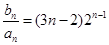 ,利用错位相减法求出
,利用错位相减法求出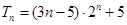 .
.
解:(1)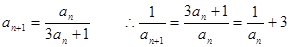
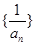 是首项a1,公差d=3的等差数列
是首项a1,公差d=3的等差数列 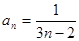
(2)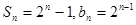
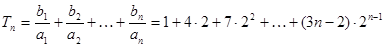
2Tn=1·2+4·22+7·22+…+(3n-2)·2n
两式相减-Tn=1+3(2+22+…+2n-1)-(3n-2)·2n
=-5-(3n-5)·2n
∴Tn=(3n-5)·2n+5
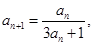 即
即 ,又
,又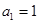 ,所以
,所以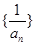 是首项a1,公差d=3的等差数列,根据等差数列的通项公式得
是首项a1,公差d=3的等差数列,根据等差数列的通项公式得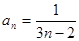 ;(2)由
;(2)由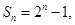 可求出
可求出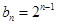 ,所以
,所以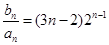 ,利用错位相减法求出
,利用错位相减法求出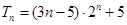 .
.解:(1)
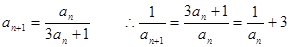
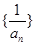 是首项a1,公差d=3的等差数列
是首项a1,公差d=3的等差数列 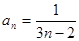
(2)
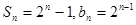
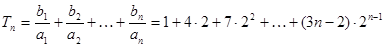
2Tn=1·2+4·22+7·22+…+(3n-2)·2n
两式相减-Tn=1+3(2+22+…+2n-1)-(3n-2)·2n
=-5-(3n-5)·2n
∴Tn=(3n-5)·2n+5

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
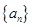 的前
的前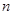 项和为
项和为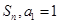 且
且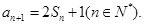
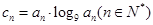 ,
,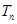 为数列
为数列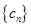 的前
的前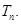
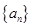 中的相邻两项
中的相邻两项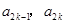 是关于
是关于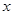 的方程
的方程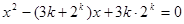 的两个根,且
的两个根,且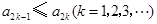 .
.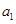 ,
,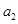 ,
,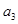 ,
,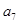 ;
; 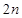 项和
项和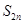 ;
;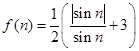 ,
,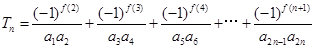 ,
,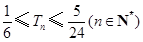 .
.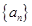 满足:
满足: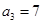 ,
,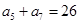 ,
,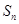 .
.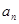 及
及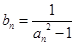 (
(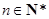 ),求数列
),求数列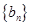 的前n项和
的前n项和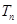 .
.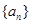 的各项均为正数,
的各项均为正数,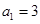 ,前
,前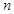 项和为
项和为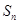 ,
,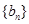 为等比数列,
为等比数列, 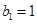 ,
,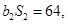
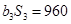 .
.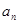 与
与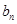 ;
;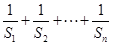 .
. 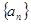 是公差不为0的等差数列,
是公差不为0的等差数列,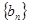 是等比数列,且
是等比数列,且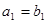 ,
,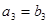 ,
,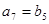 ,
,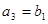
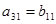
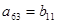
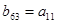
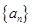 中,
中,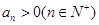 ,公比
,公比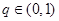 ,且
,且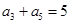 ,又
,又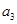 与
与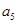 的等比中项为2.
的等比中项为2.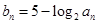 ,数列
,数列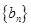 的前
的前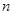 项和为
项和为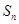 ,求数列
,求数列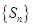 的通项公式;
的通项公式;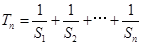 ,求
,求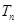 .
.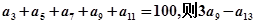 的值为( )
的值为( )