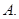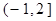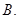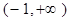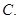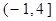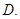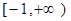题目内容
f (x)是定义在R上的奇函数,对任意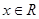 总有
总有 ,则
,则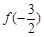 的值为( )
的值为( )
| A.0 | B.3 | C.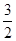 | D.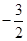 |
A
解析本题主要考查的是函数的周期性与奇偶性。由条件可知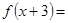
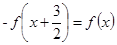 ,所以函数的周期为3,
,所以函数的周期为3,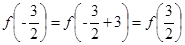 。又
。又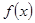 是定义在R上的奇函数,所以
是定义在R上的奇函数,所以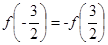 ,与上式联立解得
,与上式联立解得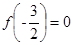 ,应选A。
,应选A。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,其最小正周期为3,且x∈(-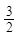 ,0)时,f(x)=log2(-3x+1),则f(2011)=( )
,0)时,f(x)=log2(-3x+1),则f(2011)=( )
| A.4 | B.2 | C.-2 | D.log27 |
设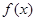 为定义在
为定义在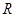 上的奇函数,当
上的奇函数,当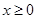 时,
时,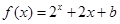 (
(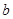 为常数),则
为常数),则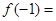 ( )
( )
| A.-3 | B.-1 | C.1 | D.3 |
函数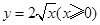 的反函数为
的反函数为
A.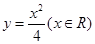 | B.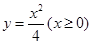 | C.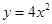 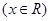 | D.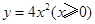 |
已知函数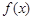 满足:①定义域为R;②
满足:①定义域为R;②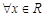 ,有
,有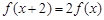 ;③当
;③当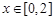 时,
时,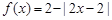 .记
.记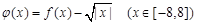 .根据以上信息,可以得到函数
.根据以上信息,可以得到函数 的零点个数为 ( )
的零点个数为 ( )
| A.15 | B.10 | C.9 | D.8 |
f(x)是定义在R上的增函数,则不等式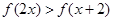 的解集是( )
的解集是( )
| A.(0 ,+∞) | B.(0 , 2) | C.(2 ,+∞) | D.(-∞,2) |
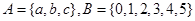 ,定义函数
,定义函数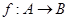 ,若
,若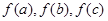 两两不相等,且
两两不相等,且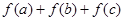 为不小于6的偶数,则满足上述条件的不同的函数
为不小于6的偶数,则满足上述条件的不同的函数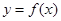 有( )个
有( )个
| A.48 | B.54 | C.60 | D.66 |
“函数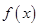 在
在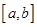 上单调”是“函数
上单调”是“函数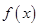 在
在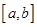 上有最大值和最小值”的( )条件.
上有最大值和最小值”的( )条件.
| A.充分但不必要 | B.必要但不充分 |
| C.充分必要 | D.既不充分也不必要 |
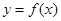 定义在
定义在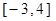 上的递增函数,且
上的递增函数,且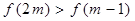 ,则实
,则实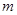 的取值范围是 ( )
的取值范围是 ( )