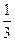题目内容
已知双曲线E的离心率为e,左、右两焦点分别为F1、F2,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 ( )
| A. | B.3 | C. | D. |
A
解析

练习册系列答案
相关题目
过抛物线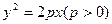 的焦点F且倾斜角为60°的直线l与抛物
的焦点F且倾斜角为60°的直线l与抛物
线在第一、四象限分别交于A、B两点,则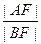 的值等于 ( )
的值等于 ( )
| A.5 | B.4 | C.3 | D.2 |
设双曲线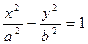 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x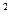 +1 只有一个公共点,则双曲线的离心率为
+1 只有一个公共点,则双曲线的离心率为 
A.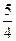 | B.5 | C.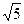 | D.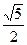 () () |
△ABC一边的两个顶点为B( 3,0),C(3,0)另两边所在直线的斜率之积为
3,0),C(3,0)另两边所在直线的斜率之积为 (
( 为常数),则顶点A的轨迹不可能落在下列哪一种曲线上 ( )
为常数),则顶点A的轨迹不可能落在下列哪一种曲线上 ( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
已知集合A= , 方程:
, 方程: 表示焦点在
表示焦点在 轴上的椭圆,则这样的不同椭圆的个数是
轴上的椭圆,则这样的不同椭圆的个数是
| A.9 | B.10 | C.18 | D.19 |
已知椭圆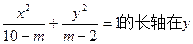 轴上,若焦距为4,则m等于 ( )
轴上,若焦距为4,则m等于 ( )
| A.4 | B.5 | C.8 | D.14 |
抛物线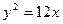 的准线与双曲线
的准线与双曲线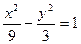 的两条渐近线所围成的三角形的面积等于( )
的两条渐近线所围成的三角形的面积等于( )
A.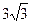 | B.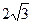 | C.2 | D. |
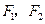 分别为双曲线
分别为双曲线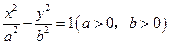 的左、右焦点,
的左、右焦点, 为双曲线右支上任一点,若
为双曲线右支上任一点,若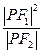 的最小值为
的最小值为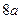 ,则该双曲线的离心率的取值范围是 ( )
,则该双曲线的离心率的取值范围是 ( )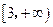
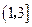

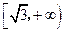
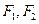 是椭圆的两个焦点,过
是椭圆的两个焦点,过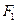 且与椭圆长轴垂直的弦交椭圆与
且与椭圆长轴垂直的弦交椭圆与 ,
, 两点,
两点,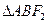 是正三角形,则椭圆的离心率是( )
是正三角形,则椭圆的离心率是( )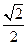 B
B 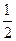 C
C 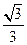 D
D