题目内容
直线l与椭圆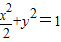 交于不同的两点P1、P2,线段P1P2的中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2(O点为坐标原点),则k1•k2的值为( )
交于不同的两点P1、P2,线段P1P2的中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2(O点为坐标原点),则k1•k2的值为( )A.
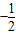
B.-1
C.-2
D.不能确定
【答案】分析:设点,代入椭圆方程,利用点差法,结合线段P1P2的中点为P,即可得到结论.
解答:解:设P1(x1,y1),P2(x2,y2),P(x,y),则x1+x2=2x,y1+y2=2y
∵x12+2y12=2,x22+2y22=2
两式相减可得:(x1-x2)×2x+2(y1-y2)×2y=0
∴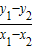 ×
×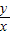 =-
=- ,
,
∵直线l的斜率为k1(k1≠0),直线OP(O是原点)的斜率为k2,
∴k1k2=- .
.
故选A.
点评:本题考查椭圆方程的性质和应用,考查点差法的运用,考查学生的计算能力,属于中档题.
解答:解:设P1(x1,y1),P2(x2,y2),P(x,y),则x1+x2=2x,y1+y2=2y
∵x12+2y12=2,x22+2y22=2
两式相减可得:(x1-x2)×2x+2(y1-y2)×2y=0
∴
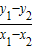 ×
×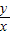 =-
=- ,
,∵直线l的斜率为k1(k1≠0),直线OP(O是原点)的斜率为k2,
∴k1k2=-
 .
.故选A.
点评:本题考查椭圆方程的性质和应用,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2009•淄博一模)已知中心在原点、焦点在x轴上的椭圆,其离心率e=
(2009•淄博一模)已知中心在原点、焦点在x轴上的椭圆,其离心率e=