题目内容
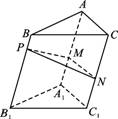
20.如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:
DE2=DF2+EF2-2DF·EFcosDFE.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面
积与其中两个侧面所成的二面角之间的关系式,并予以证明.

20.[证明](1)∵CC1∥BB1,
∴CC1⊥PM,CC1⊥PN,且PM、PN相交于点P,
∴CC1⊥平面PMN.
∵MN![]() 平面PMN,∴CC1⊥MN.
平面PMN,∴CC1⊥MN.
[解](2)在斜三棱柱ABC-A1B1C1中,有
S![]() =S
=S![]() +S
+S![]() -2S
-2S![]() S
S![]() cosα.
cosα.
其中α为平面CC1B1B与平面CC1A1A所组成的二面角.
∵CC1⊥平面PMN,
∴平面CC1B1B与平面CC1A1A所组成的二面角为∠MNP.
在△PMN中,PM2=PN2+MN2-2PN·MNcosMNP,
PM2·CC![]() =PN2·CC
=PN2·CC![]() +MN2·CC
+MN2·CC![]() -2(PN·CC1)·(MN·CC1) cosMNP, 由于S
-2(PN·CC1)·(MN·CC1) cosMNP, 由于S![]() =PN·CC1,S
=PN·CC1,S![]() =MN·CC1,S
=MN·CC1,S![]() =
=
PM·BB1及CC1=BB1,
则S![]() =S
=S![]() +S
+S![]() -2S
-2S![]() S
S![]() cosα.
cosα.

练习册系列答案
相关题目
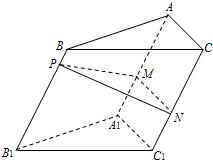 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.