题目内容
函数f(x)=ax3+(a-1)x2+48(a-2)x+b的图象关于原点成中心对称图形,则f(x)在[-4,4]上的单调性是( )
| A、[-4,0]上是增函数[0.4]上是减函数 |
| B、增函数 |
| C、减函数 |
| D、不具备单调性 |
考点:二次函数的性质
专题:函数的性质及应用,导数的综合应用
分析:根据已知条件容易求得a=1,b=0,所以得到f(x)=x3-48x,f′(x)=3x2-48,所以x∈[-4,4]时,f′(x)≤0,所以得出f(x)在[-4,4]上是减函数.
解答:
解:∵f(x)图象关于原点成中心对称图形;
∴f(-x)=-f(x);
∴a=1,b=0;
∴f(x)=x3-48x;
∴f′(x)=3x2-48;
∵x∈[-4,4];
∴f′(x)≤0;
∴f(x)在[-4,4]上单调递减.
故选C.
∴f(-x)=-f(x);
∴a=1,b=0;
∴f(x)=x3-48x;
∴f′(x)=3x2-48;
∵x∈[-4,4];
∴f′(x)≤0;
∴f(x)在[-4,4]上单调递减.
故选C.
点评:考查图象关于原点对称时,f(-x)与f(x)的关系,以及根据导数符号判断函数单调性的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
中自变量x的取值范围是( )
| x-2 |
| A、x>2 | B、x<2 |
| C、x≥2 | D、x≤2 |
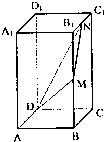 如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )
如图,在长方体ABCD-A1B1C1D1中,M、N分别为BB1、B1C1的中点,P为平面DMN内的一动点,若点P到平面BCC1B1的距离等于PD时,则点的轨迹是( )| A、圆或圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、椭圆的一部分 |
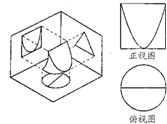 一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )
一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )