题目内容
在二项式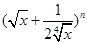 的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,则有理项都不相邻的概率为
的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,则有理项都不相邻的概率为
A.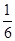 | B.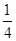 | C.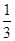 | D.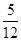 |
D
解析试题分析:展开式通项为 ,所以展开式的前三项系数分别为
,所以展开式的前三项系数分别为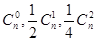 ,因为前三项的系数成等差数列,所以
,因为前三项的系数成等差数列,所以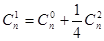 ,解得
,解得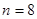 ,所以展开式共有9项,所以展开式
,所以展开式共有9项,所以展开式 ,当
,当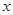 的指数为整数时,为有理项,所以当
的指数为整数时,为有理项,所以当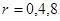 时,
时,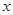 的指数为整数即第1,5,9项为有理数共有3个有理项,所以有理项不相邻的概率
的指数为整数即第1,5,9项为有理数共有3个有理项,所以有理项不相邻的概率
考点:二项式定理;等差数列的性质;等可能事件的概率
点评解决排列、组合问题中的不相邻问题时,先将没有限制条件的元素排起来;再将不相邻的元素进行插空.

练习册系列答案
相关题目
有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有( )不同的装法.
| A.240 | B.120 | C.600 | D.360 |
从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有( )
| A.120种 | B.96种 | C.60种 | D.48种 |
从 台甲型和
台甲型和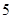 台乙型电视机中任意取出
台乙型电视机中任意取出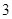 台,其中至少有甲型与乙型电视机各
台,其中至少有甲型与乙型电视机各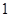 台,则不同的取法共有( )
台,则不同的取法共有( )
A.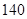 种 种 | B.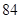 种 种 | C. 种 种 | D.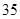 种 种 |
将4个不同的球放入3个不同的盒中,每个盒内至少有1个球,则不同的放法种数为( )
| A.24 | B.36 | C.48 | D.96 |
 且
且 ,则乘积
,则乘积 等于
等于
A. | B. | C. | D. |
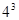
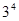


 种,选出三人班级委的选法共有
种,选出三人班级委的选法共有 种,则
种,则 是 ( )
是 ( )