题目内容
已知P（x，y）满足约束条件
，O为坐标原点，A（3，4），则|
|•cos∠AOP的最大值是
．
|
| OP |
| 11 |
| 5 |
| 11 |
| 5 |
分析：连接OA、OP、AP，由余弦定理的推论把cos∠AOP化为
，代入两点间的距离公式后展开整理，则|
|•cos∠AOP的值化为
，进一步运用线性规划知识求3x+4y的最大值即可．
|
| ||||||
2|
|
| OP |
| 3x+4y |
| 5 |
解答：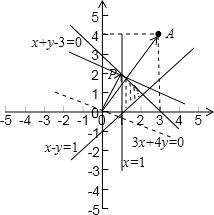
解：|
|=
=5，|
|2=x2+y2，|
|2=(x-3)2+(y-4)2=x2+y2-6x-8y+25，
|
|•cos∠AOP=|
|×
=
=
，
因为P（x，y）满足约束条件
，
可行域如图，
要使
最大，首先作出直线3x+4y=0，由图看出当直线平移经过直线x=1和x+y-3=0的交点（1，2）时3x+4y最大，
则
最大，值为
=
．
故答案为
．
解：|| OA |
| 32+42 |
| OP |
| AP |
|
| OP |
| OP |
|
| ||||||
2|
|
=
| 25+x2+y2-x2-y2+6x+8y-25 |
| 10 |
| 3x+4y |
| 5 |
因为P（x，y）满足约束条件
|
可行域如图，
要使
| 3x+4y |
| 5 |
则
| 3x+4y |
| 5 |
| 3×1+4×2 |
| 5 |
| 11 |
| 5 |
故答案为
| 11 |
| 5 |
点评：本题考查了简单的线性规划，考查了平面向量数量积的含义，考查了数学转化思想和数形结合思想，解答此题的关键是把要求的式子转化为含P点坐标的代数式，进一步运用线性规划知识解决，此题有一定难度．
练习册系列答案
相关题目
，O为坐标原点，A（3，4），则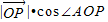
的最大值是 ．
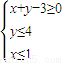，Q是x轴上一个动点，定点R（2，3），则|PQ|+|QR|可以取到的最小值是 ．