题目内容
已知直线l1:ax+3y+1=0,l2:x+(a-2)y+a=0.
(1)若l1⊥l2,求实数a的值;
(2)当l1∥l2时,求直线l1与l2之间的距离.
解:(1)由l1⊥l2可得:a+3(a-2)=0,…4分
解得 ;…6分
;…6分
(2)当l1∥l2时,有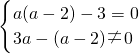 ,…8分
,…8分
解得a=3,…9分
此时,l1,l2的方程分别为:3x+3y+1=0,x+y+3=0即3x+3y+9=0,
故它们之间的距离为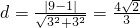 .…12分.
.…12分.
分析:(1)由垂直可得a+3(a-2)=0,解之即可;(2)由平行可得a=3,进而可得直线方程,代入距离公式可得答案.
点评:本题考查直线的一般式方程的平行和垂直关系,涉及平行线间的距离公式,属基础题.
解得
 ;…6分
;…6分(2)当l1∥l2时,有
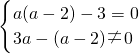 ,…8分
,…8分解得a=3,…9分
此时,l1,l2的方程分别为:3x+3y+1=0,x+y+3=0即3x+3y+9=0,
故它们之间的距离为
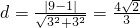 .…12分.
.…12分.分析:(1)由垂直可得a+3(a-2)=0,解之即可;(2)由平行可得a=3,进而可得直线方程,代入距离公式可得答案.
点评:本题考查直线的一般式方程的平行和垂直关系,涉及平行线间的距离公式,属基础题.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目