题目内容
对于函数y=ex,曲线y=ex在与坐标轴交点处的切线方程为y=x+1,由于曲线 y=ex在切线y=x+1的上方,故有不等式ex≥x+1.类比上述推理:对于函数y=lnx(x>0),有不等式( )A.lnx≥x+1(x>0)
B.lnx≤1-x(x>0)
C.lnx≥x-1(x>0)
D.lnx≤x-1(x>0)
【答案】分析:求出导数和函数图象与轴的交点坐标,再求出在交点处的切线斜率,代入点斜式方程求出切线方程,再与函数的图象位置比较,得到不等式.
解答:解:由题意得,y′=lnx=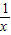 ,且y=lnx图象与x轴的交点是(1,0),
,且y=lnx图象与x轴的交点是(1,0),
则在(1,0)处的切线的斜率是1,
∴在(1,0)处的切线的方程是y=x-1,
∵切线在y=lnx图象上方(x>0),
∴x-1≥lnx(x>0),
故选D.
点评:本题考查了导数的几何意义,即在某点处的切线斜率是该点处的导数值,以及对数函数图象的特点等.
解答:解:由题意得,y′=lnx=
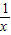 ,且y=lnx图象与x轴的交点是(1,0),
,且y=lnx图象与x轴的交点是(1,0),则在(1,0)处的切线的斜率是1,
∴在(1,0)处的切线的方程是y=x-1,
∵切线在y=lnx图象上方(x>0),
∴x-1≥lnx(x>0),
故选D.
点评:本题考查了导数的几何意义,即在某点处的切线斜率是该点处的导数值,以及对数函数图象的特点等.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
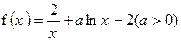
 y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K]
y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K] 成立,试求a的取值范围;
成立,试求a的取值范围;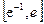 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。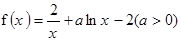
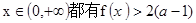 成立,试求a的取值范围;
成立,试求a的取值范围;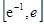 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。