题目内容
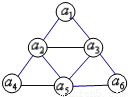
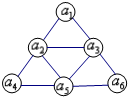如图，将等比数列{an}的前6项填入一个三角形的顶点及各边中点的位置，且在图中每个三角形的顶点所填的三项也成等比数列，数列{an}的前2013项和S2013=4026，则满足n an＞ann的n的值为（ ）分析：先根据题意得到数列{an}是常数数列，再根据S2013=4026可求出{an}的通项，然后求出满足n an＞ann的n的值即可．
解答：解：∵数列{an}是等比数列，每个三角形的顶点所填的三项也成等比数列，
∴数列{an}是常数数列
∵S2013=4026
∴an=2
∵n an＞ann
∴n2＞2n满足条件的n的值为3
故选B．
∴数列{an}是常数数列
∵S2013=4026
∴an=2
∵n an＞ann
∴n2＞2n满足条件的n的值为3
故选B．
点评：本题主要考查了等比数列的通项公式，以及等比数列的前n项和，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
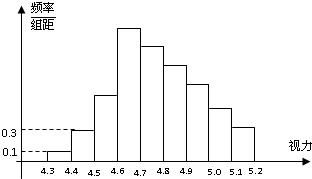为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为（ ）| A、0.27，78 | B、0.27，83 | C、2.7，78 | D、2.7，83 |
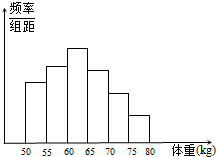（2008•深圳二模）某校对高三年级的学生进行体检，现将高三男生的体重（单位：kg）数据进行整理后分成六组，并绘制频率分布直方图（如图所示）．已知图中从左到右第一、第六小组的频率分别为0.16、0.07，第一、第二、第三小组的频率成等比数列，第三、第四、第五、第六小组的频率成等差数列，且第三小组的频数为100，则该校高三年级的男生总数为（ ）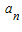
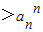的n的值为（ ）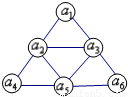
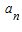
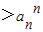的n的值为（ ）