题目内容
下列说法中错误的个数是( )
①一个命题的逆命题为真,它的否命题也一定为真;
②命题“?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0”;
③“矩形的两条对角线相等”的逆命题是真命题;
④“x≠3”是“|x|≠3”成立的充分条件.
①一个命题的逆命题为真,它的否命题也一定为真;
②命题“?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0”;
③“矩形的两条对角线相等”的逆命题是真命题;
④“x≠3”是“|x|≠3”成立的充分条件.
分析:①由四种命题之间的关系即可选出;
②命题“?x∈R,p(x)”的否定应是“?x0∈R,¬p(x0)”,故判断②的真假;
③对其逆命题可举出反例“对角线相等的四边形可以是等腰梯形”;
④可举出反例.
②命题“?x∈R,p(x)”的否定应是“?x0∈R,¬p(x0)”,故判断②的真假;
③对其逆命题可举出反例“对角线相等的四边形可以是等腰梯形”;
④可举出反例.
解答:解:①∵一个命题的逆命题和否命题是逆否的关系,故一个命题的逆命题为真,它的否命题也一定为真,故①正确;
②命题“?x∈R,x2-x≤0”的否定应是“?x∈R,x2-x>0”,故②不正确;
③“矩形的两条对角线相等”的逆命题是“对角线相等的四边形是矩形”不是真命题,因为对角线相等的四边形可以是等腰梯形,故③不正确;
④当x≠3时,取x=-3,则|x|=3,所以“x≠3”不是“|x|≠3”成立的充分条件,故④不正确.
综上可知:不正确的是②③④.
故选C.
②命题“?x∈R,x2-x≤0”的否定应是“?x∈R,x2-x>0”,故②不正确;
③“矩形的两条对角线相等”的逆命题是“对角线相等的四边形是矩形”不是真命题,因为对角线相等的四边形可以是等腰梯形,故③不正确;
④当x≠3时,取x=-3,则|x|=3,所以“x≠3”不是“|x|≠3”成立的充分条件,故④不正确.
综上可知:不正确的是②③④.
故选C.
点评:正确理解四种命题之间的关系和充分必要条件的意义是解题的关键.

练习册系列答案
相关题目
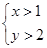 是
是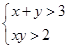 的充要条件;④
的充要条件;④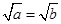 与
与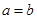 是等价的;⑤“
是等价的;⑤“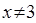 ”是“
”是“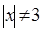 ”成立的充分条件.
”成立的充分条件.