题目内容
已知椭圆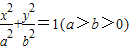 的右焦点F(1,0),离心率为e.
的右焦点F(1,0),离心率为e.(1)若
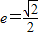 ,求椭圆方程;
,求椭圆方程;(2)设直线y=kx(k>0)与椭圆相交于A,B两点,M,N分别为线段AF,BF的中点,若坐标原点O在以MN为直径的圆上.
(i)将k表示成e的函数;
(ii)当
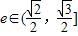 时,求k的取值范围.
时,求k的取值范围.
【答案】分析:(1)利用椭圆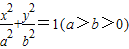 的右焦点F(1,0),
的右焦点F(1,0),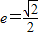 ,建立方程,可得椭圆的几何量,从而可得椭圆方程;
,建立方程,可得椭圆的几何量,从而可得椭圆方程;
(2))(i)直线y=kx(k>0)与椭圆方程联立,求出A,B的坐标,利用坐标原点O在以MN为直径的圆上,可得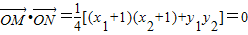 ,化简可得结论;
,化简可得结论;
(ii)当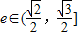 时,结合(i)的结论,即可求k的取值范围.
时,结合(i)的结论,即可求k的取值范围.
解答:解:(1)∵椭圆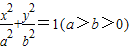 的右焦点F(1,0),
的右焦点F(1,0),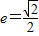 ,
,
∴
∴c=1,a=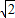
∴ =1
=1
∴椭圆方程为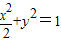 ;
;
(2)(i)直线y=kx(k>0)与椭圆方程联立,可得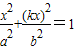
设A(x1,y1),B(x2,y2),则x1=-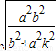 ,x2=
,x2=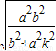
∴y1=-k•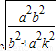 ,y2=k•
,y2=k•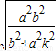
∵坐标原点O在以MN为直径的圆上
∴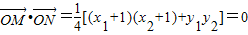
∴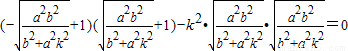
∴
∴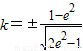 ;
;
(ii)∵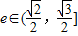 ,∴
,∴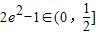
设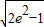 =t,则t∈
=t,则t∈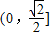
∴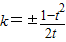 ,∴
,∴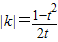
∵t∈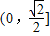 ,∴
,∴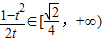
∴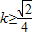 或
或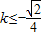 .
.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.
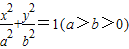 的右焦点F(1,0),
的右焦点F(1,0),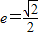 ,建立方程,可得椭圆的几何量,从而可得椭圆方程;
,建立方程,可得椭圆的几何量,从而可得椭圆方程;(2))(i)直线y=kx(k>0)与椭圆方程联立,求出A,B的坐标,利用坐标原点O在以MN为直径的圆上,可得
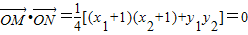 ,化简可得结论;
,化简可得结论;(ii)当
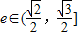 时,结合(i)的结论,即可求k的取值范围.
时,结合(i)的结论,即可求k的取值范围.解答:解:(1)∵椭圆
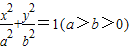 的右焦点F(1,0),
的右焦点F(1,0),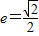 ,
,∴

∴c=1,a=
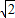
∴
 =1
=1∴椭圆方程为
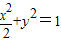 ;
;(2)(i)直线y=kx(k>0)与椭圆方程联立,可得
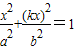
设A(x1,y1),B(x2,y2),则x1=-
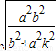 ,x2=
,x2=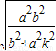
∴y1=-k•
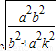 ,y2=k•
,y2=k•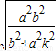
∵坐标原点O在以MN为直径的圆上
∴
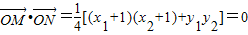
∴
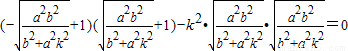
∴

∴
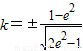 ;
;(ii)∵
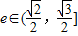 ,∴
,∴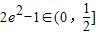
设
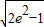 =t,则t∈
=t,则t∈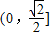
∴
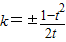 ,∴
,∴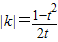
∵t∈
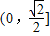 ,∴
,∴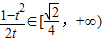
∴
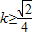 或
或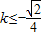 .
.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
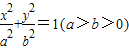 的右焦点F(1,0),离心率为e.
的右焦点F(1,0),离心率为e.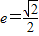 ,求椭圆方程;
,求椭圆方程;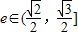 时,求k的取值范围.
时,求k的取值范围.